Arkusz 13 Zad 2

Nie rozumiem jak w drugim przypadku dojść do tego, że x<-3.
Matematyka nierówności Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
czy w książce jest poprawna odpowiedź? bo wychodzi mi tak jak koledze wyżej a odpowiedź jest inna
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No bo właśnie to -12<x<-3 jest dziedziną tego przypadku. Potem zwyczajnie to rozwiązuję, przy czym nie jestem pewien czy dobrze robię zmieniając znak nierówności przy podnoszeniu do kwadratu, bo jedna ze stron jest nieujemna.
I jeśli to jest dobrze to mam jeszcze ogólniejsze pytanie: czy podnosząc nierówność ujemną po obu stronach do kwadratu także zmienia się znak?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Finalna odpowiedź w kryteriach jest na pewno ok. Jaka ci wyszła @mariajurka ?
@Artur - sprawdź sobie ten warunek na prostym przypadku:
-3 > -10
teraz podnieś do kwadratu i zastanów się czy musisz zmienić znak czy nie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Muszę zmienić znak. Dlatego robiąc to uważam, że wyszła mi poprawna odpowiedź.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur - sprawdź czym różnią się twoja odpowiedź - od odpowiedzi z kryteriów. Tzn. jaką liczbą np. zawiera w rozwiązaniu odpowiedź z kryteriów która nie zawiera twoja (lub na odwrót), a następnie podstaw pod nierówność z polecenia - będziemy wiedzieć czy w kryteriach jest błąd czy u ciebie :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
"Rozwiązanie nierówności w przedziale x<-3: x<-3" Nie rozumiem skąd się to bierze i nie ma za bardzo jak to sprawdzić, bo w odpowiedziach nie ma obliczeń. Wychodzi na to, że aby było x<-3 to delta<0 a mi wyszła dodatnia.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przecież wyszła ci poprawna delta Artur. Rozwiąż do końca tę nierówność a zobaczysz że dla tego przedziału x < -3 będzie rozwiązaniem x<-3 a dokładny przedział to będzie z uwzględnieniem założenia pierwiastka:
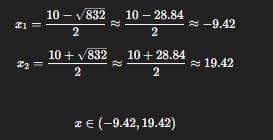
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
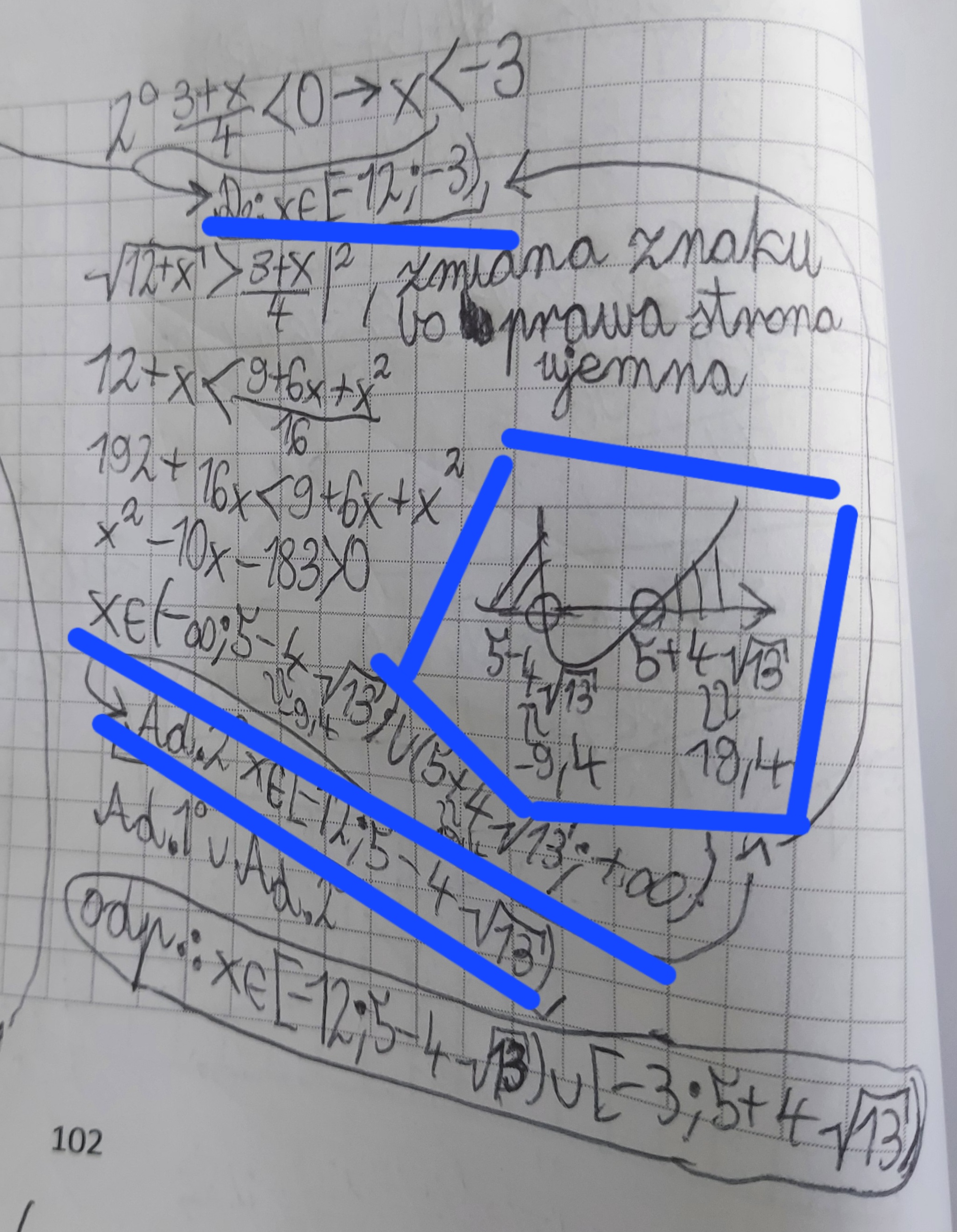
A jednak podkreślone działania prowadzą u mnie do innego wyniku niż x<-3.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zmiana znaku bo prawa strona ujemna, dlaczego prawa storna jest u ciebie ujemna skoro x<-3 ?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No właśnie dlatego, że skoro x<-3 to 3+x<0, więc (3+x)/4<0.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak to się zgadza, zauważ teraz co wychodzi z naszych warunków:
Skoro mamy taką nierówność:
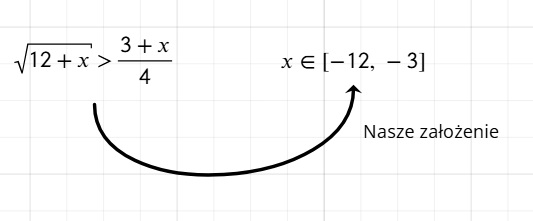
Zauważ, że dla naszej dziedziny - zawsze prawa strona będzie równa 0 lub będzie ujemna z kolei lewa strona zawsze będzie nieujemna.
Dla skrajnego przypadku kiedy prawa strona będzie równa zeru, lewa zawsze będzie dodatnia. Zatem nierówność jest zawsze spełniona w calej dziedzinie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ale właśnie prawa strona nigdy nie może być równa zeru skoro pierwiastek>=0 i pierw(12+x)>(3+x)/4 to prawa strona jest zawsze ujemna.
Ale mimo to chyba powinno mi to wyjść z obliczeń, chyba że coś źle zapisałem.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur mylisz założenia z tym co może się wydarzyć. To że do dziedziny należy x=3 nie znaczy, że dla x=3 nierówność będzie spełniona.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie rozumiem tego. Przecież ewidentnie z drugiego przypadku wychodzi: -12<x<5-4*pierw(13).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przecież rozpisałem ci tutaj drugi przypadek: 
I opisałem dlaczego rozwiązanie jest takie a nie inne, która część jest niezrozumiała ?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ale po rozwiązaniu tej nierówności też powinna wyjść poprawna odpowiedź do tego przypadku.
Poza tym chyba przy x zarówna w 1 jak i w 2 przypadku powinny być nawiasy otwarte, bo inaczej wyjdzie sprzeczność (0>0).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dlatego ci ta nierówność nie wychodzi, przeanalizuj ten przypadek:

- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ale przecież zmieniam znak w 2 przypadku podnosząc do kwadratu, mam to nawet podpisane.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No właśnie dlatego wychodzą ci błędne rezultaty.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ale ustaliliśmy, że przy podnoszeniu do kwadratu nierówności, w której jedna strona jest ujemna zmieniamy znak nierówności. Tak też zrobiłem i przez to mam błąd?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur tłumaczę, że nie zawsze to prawda spójrz:
2 > -9 (PRAWDA)
obustronnie podnosimy do kwadratu:
4 < 18 (PRAWDA)
Ale może być tak:
2 > -1
Podnosimy do kwadratu: 4< 1 FAŁSZ
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli trzeba sprawdzić co jest na moduł większe. Ale nie rozumiem tego jak to zrobić w tym drugim przypadku.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dokładnie tak jak opisałem to wyżej. W moim komentarzu.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chodzi o ten komentarz? "Tak to się zgadza, zauważ teraz co wychodzi z naszych warunków:
Skoro mamy taką nierówność:

Zauważ, że dla naszej dziedziny - zawsze prawa strona będzie równa 0 lub będzie ujemna z kolei lewa strona zawsze będzie nieujemna.
Dla skrajnego przypadku kiedy prawa strona będzie równa zeru, lewa zawsze będzie dodatnia. Zatem nierówność jest zawsze spełniona w calej dziedzinie."
Bo jeśli tak to rozumiem, że trzeba sprawdzić wartości graniczne dla x=-3 i x=-12
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No bo rozumiem jakby zamysł, ale chciałbym to jakoś obliczyć a nie tak rozpisywać jak powyżej.
Poza tym biorąc pod uwagę, że nawias tej nierówności jest > (a nie >=) to prawa strona nie może być nigdy równa zero tylko zawsze ujemna bo lewa strona jest nieujemna (wartość bezwzględna), więc z tego co rozumiem to graniczny przypadek byłby dla 0 po lewej a po prawej liczba ujemna.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak zgadza się. To jest graniczny przypadek.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A da się to jakoś zwyczajnie obliczyć, żeby nie rozumować w ten sposób? Czy nie wiadomo byłoby właściwie czy zmieniać znak nierówności czy też nie i dlatego musimy tak robić?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Można np przerzucić wszystko na jedną stronę i przeanalizować funkcję (monotoniczność) pochodna itd.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zapisałeś przecież x<-3 ? Mógłbyś sprecyzować o co dokładnie pytasz?