Arkusz 13 zadanie 11
Zadanie 11 (5 pkt)
Podstawa ostrostupa jest trójkat równoramienny. Podstawa tego trójkata ma 4 cm, a miara kata naprzeciwko tej podstawy wynosi 45°. Pozostale krawedzie tego ostroslupa sa równej dlugosei.
Oblicz objetosé danej bryly.
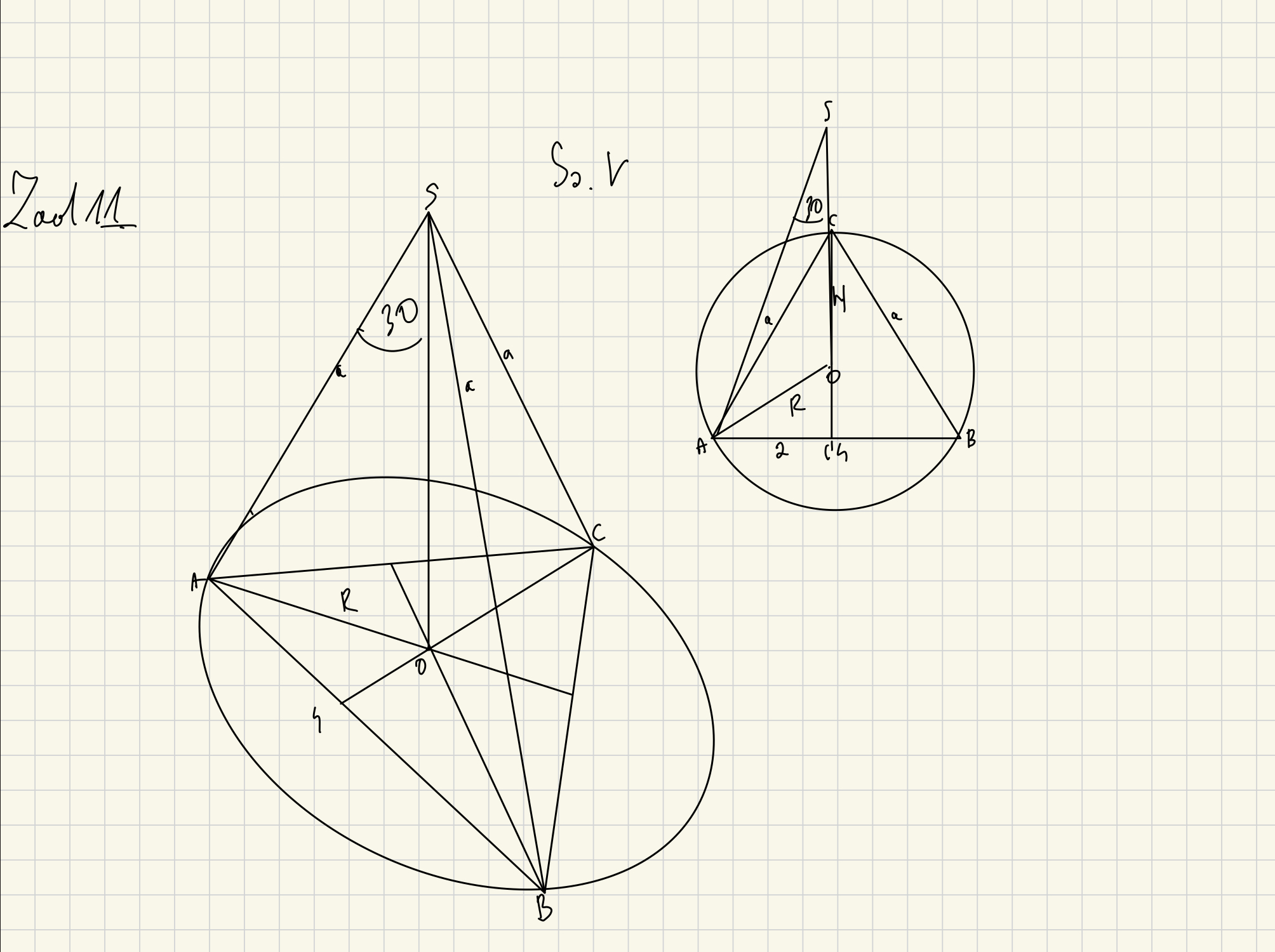Nie wiem jak się zabrać za to zadanie i wgl jak co obliczać skoro jest trójkąt równoramienny.
Matematyka stereometria Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W jaki sposób moge obliczyc wysokosc tego ostroslupa skoro tylko wiem że są rownej dlugosci krawedzię boczne? obliczylem pole podstawy, promien okregu opisanego jak i pozostale boki podstawy ale zacialem sie i nie wiem jak obliczyc wysokosc ostroslupa?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Według mnie źle mogłeś zinterpretować zadanie mamy podaną jedną krawędź ostrosłupa (podstawę trójkąta równoramiennego która ma długość 4) a następnie mamy informacje że pozostałe krawędzie tego ostrosłupa są równej długości a więc wystarczy że z tw. cos policzymy długość jednego z ramion w podstawie i mamy wszystko aby obliczyć wysokość ostrosłupa z pitagorasa to_co_wyjdzie_z_tw_cos^2 - R^2 = H^2
Ps. W razie wątpliwości pisz
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Własnie nie umiem obliczyc wykosoci ostrostlupa skoro jedyne co wiemy o krawedziach bocznych że są rownej dlugosci i tylko tyle. jakby wyglądalo rownanie pitagorasa z wykoscią ostroslupa?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. Masz podaną jedną krawędź ostrosłupa która wynosi 4 pozostałe są równej długości więc podstawiamy przykładowo x
2. W podstawie obliczamy z tw. Cos x z równania 4^2=x^2+x^2-2x^2cos45
3.Z tego wyliczasz x
4.Teraz musimy zauważyć że ramię trójkąta w podstawie jest tej samej długości co krawędź boczna w ostrosłupie (wiemy to z treści "pozostałe krawędzie są równej długości")
5.I teraz już wiedząc ile wynosi krawędź boczna tworzymy tw Pitagorasa z krawędzią boczną ostrosłupa promieniem okręgu opisanego oraz wysokością ostrosłupa
Ps. W razie pytań pisz
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Cześć! Mamy trójkąt równoramienny więc sugerowałbym aby zacząć od policzenia wszystkich długości podstawy można to zrobić np. twierdzeniem cosinusa 4^2=a^2+a^2-2a^cos45stopni jak otrzymamy wszystkie długości podstawy to lecimy z polem a potem wyliczamy R ze wzoru abc/4R=P jak mamy obliczone R to jesteśmy już prawie w domu przechodzimy do obliczenia wysokości podstawiamy pod wzór na objętość i mamy wynik.
Ps. W razie pytań pisz