Arkusz 15 Zad 6

Co masz na myśli "chyba w ogóle te warunki nie do końca zgadzają mi się z podanymi odpowiedziami" ? Sprawdziłeś czym różnią się warunki - dlaczego w kryteriach są takie a u ciebie inne ?

Jeżeli warunki masz inne niż w odpowiedziach to zastanów się czy są poprawne i równoważne - jeżeli takie same to szukaj błędu obliczeniowego.

Sprawdziłem i warunki są różne, ale nie wiem dlaczego. Rozwiązania należą do przedziału (1,5) zatem x1+x2>2 ; x1+x2<10 ; (x1-1)*(x2-1)>0 ; (x1-5)*(x2-5)>0. To nie jest do końca tożsame z warunkami podanymi w odpowiedziach, ale nie wiem dlaczego tam są inne warunki skoro te odpowiadają treści zadania.

nie rozumiem tych warunków w odpowiedziach, dlaczego są takie a nie inne?

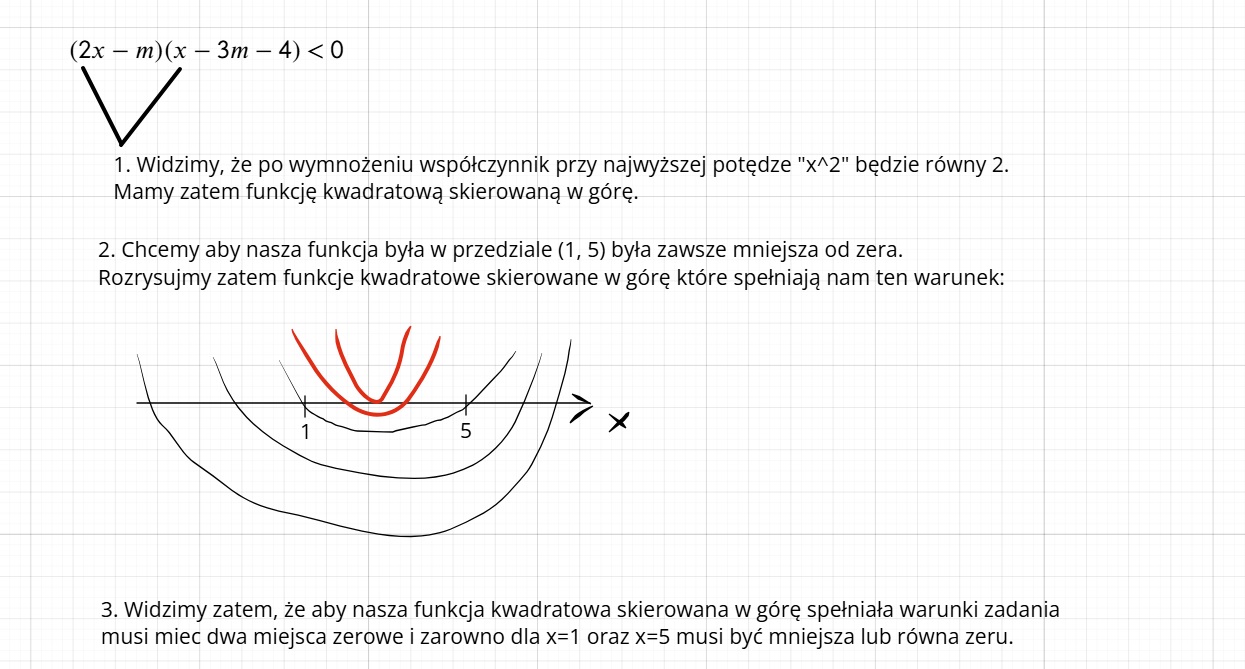
Wyjaśnienie warunków w odpowiedziach:

Czyli nie jest to tożsame z moimi warunkami? Bo nie rozumiem gdzie jest rozbieżność. 

Czy da się to zadanie rozwiązać bez takiego rysunku?

Skoro wychodzą ci błędne wyniki to musi w warunkach być nieścisłość. 

Nie musisz rysować rysunku, technika z warunkami w których zapisujemy, że dla danego argumentu funkcja musi być większa lub mniejsza od zera to częsta praktyka, rysunek to część dla nas pomocna.

A jest Pan w stanie powiedzieć czym różnią się moje warunki od tych podanych w odpowiedziach?

Brakuje ci warunków tych z kryteriów - w tym się różnią. 
Jeżeli chodzi o twoje warunki ciężko powiedzieć w jaki sposób je dobierałeś - jeżeli jesteś w stanie wyjaśnić po kolei z uzasadnieniem każdy warunek - tzn. dlaczego taki a nie inny i w jaki sposób gwarantuje nam on spełnienie warunków zadania to będzie mi łatwiej wskazać ci błąd. Przykładowo twój warunek x1 + x2 > 2 ? Co on nam daje ? Przecież gdy x1 = 50 a x2 = 100 to warunki zadania nie są spełnione.

Faktycznie, nie mogłem znaleźć takiego kontrprzykładu. A czy da się jeszcze w jakiś inny sposób to rozwiązać niż ten związany z rysunkiem?

To najprostsze warunki.

Co gdyby w tej nierówności zamiast "<" było "<="? Czy warunki pozostałyby takie same?

Zastanów się artur, co oznacza <= ?

Mniejszy lub równy. No i właśnie nie mogę sobie wyobrazić tego jak mogłyby się zmienić te warunki.

Te warunki akceptują miejsce zerowe.

A właściwie to teraz myślę, że byłoby jednak chyba f(1)<0 i f(5)<0, bo przedział (1;5) jest otwarty.

Czy ogólnie w tym zadaniu nie powinien być jeszcze warunek, że 1<p<5, gdzie p to x-owa współrzędna wierzchołka paraboli? W podobnym zadaniu z arkusza pazdro trzeba było zapisać takie warunki:

A dlaczego uważasz, że te warunki nie są wystarczające ? Czy potrafisz narysować taką funkcję kwadratową która spełnia te warunki a jej wierzchołek nie znajduje się pomiędzy tymi wartościami ? Jeżeli jesteś w stanie to tak powinieneś dopisać ten warunek. jeżeli nie jesteś to nie jest to potrzebne.

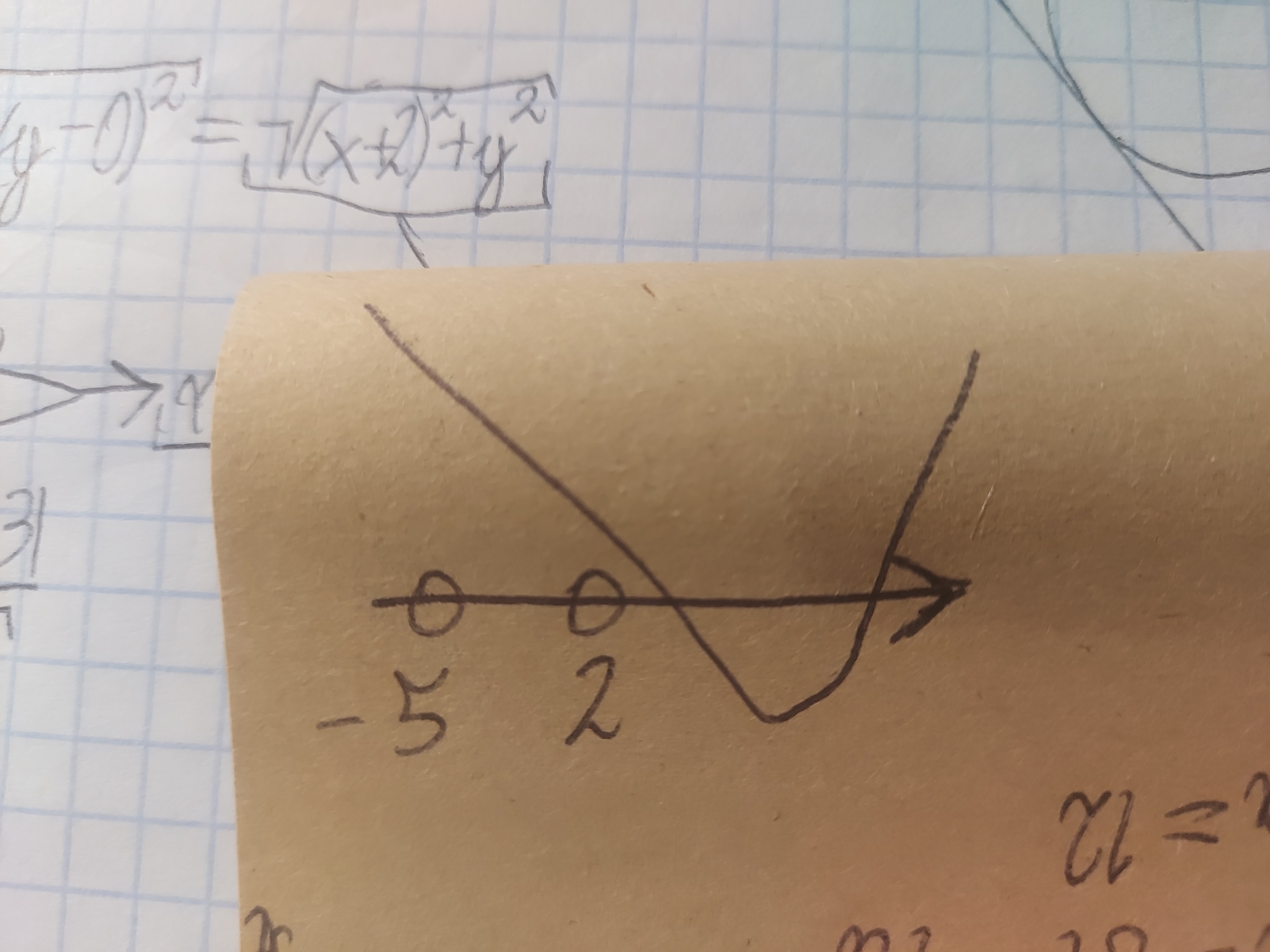
W tym zadaniu z Pazdro byłoby coś takiego jak powyżej. Ale tutaj faktycznie nie umiem sobie tego wyobrazić, żeby ten wierzchołek mógł nie leżeć pomiędzy 1 a 5 i nie wiem dlaczego nie da się tutaj zapewne podać takiego kontrprzykładu a tam się dało. Czy to dlatego, że tam była równość a tu jest nierówność?

Nie znam polecenia z tamtego zadania więc nie odpowiem ci na to pytanie.

Wysłałem treść tego polecenia 2 komentarze wyżej. "Wyznacz wszystkie wartości parametru k..."

Potrzebny jest warunek z wierzchołkiem - narysuj to sobie.

Ale w zadaniu, którego dotyczy ten post brakuje potrzebny jest ten warunek z wierzchołkiem?

Bo jeśli chodzi o zadanie z Pazdro to już powyżej mam narysowany kontrprzykład, dzięki któremu wiem, że należy taki warunek dopisać. A w tym zadaniu nie umiem podać takiego typu kontrprzykładu o ile on istnieje.

Przecież masz w kryteriach do tego zadania podane warunki. Nie ma tam nic o wierzchołku.

Dlatego pytam się, bo nie mogę zauważyć tego czym różni się to zadanie od tego z pazdro skoro tu nie trzeba używać warunku z wierzchołkiem a tam już tak?

Tam mamy nierówność a tu równanie.

Narysowałem ci przykład 1) następnie przykład 2) z dokładnym rozróżnieniem.

Sam doszedłeś do wniosku, które warunki są wystarczające a które nie - na czym dalej polega problem ?

Na tym jak stwierdzać kiedy potrzeba dodatkowo warunku z wierzchołkiem w tego typu zadaniach?

Tak jak pisałem, kiedy jest nierówność to nie trzeba, kiedy jest równość to trzeba.

Ale przecież w zadaniu, którego dotyczy ten post gdyby była równość to warunki wyglądałyby tak samo chyba.

Dlaczego ?

Mi się wydaje, że tak po prostu będzie jeśli chcemy aby ta wartość funkcji była równa zero w przedziale (1; 5).

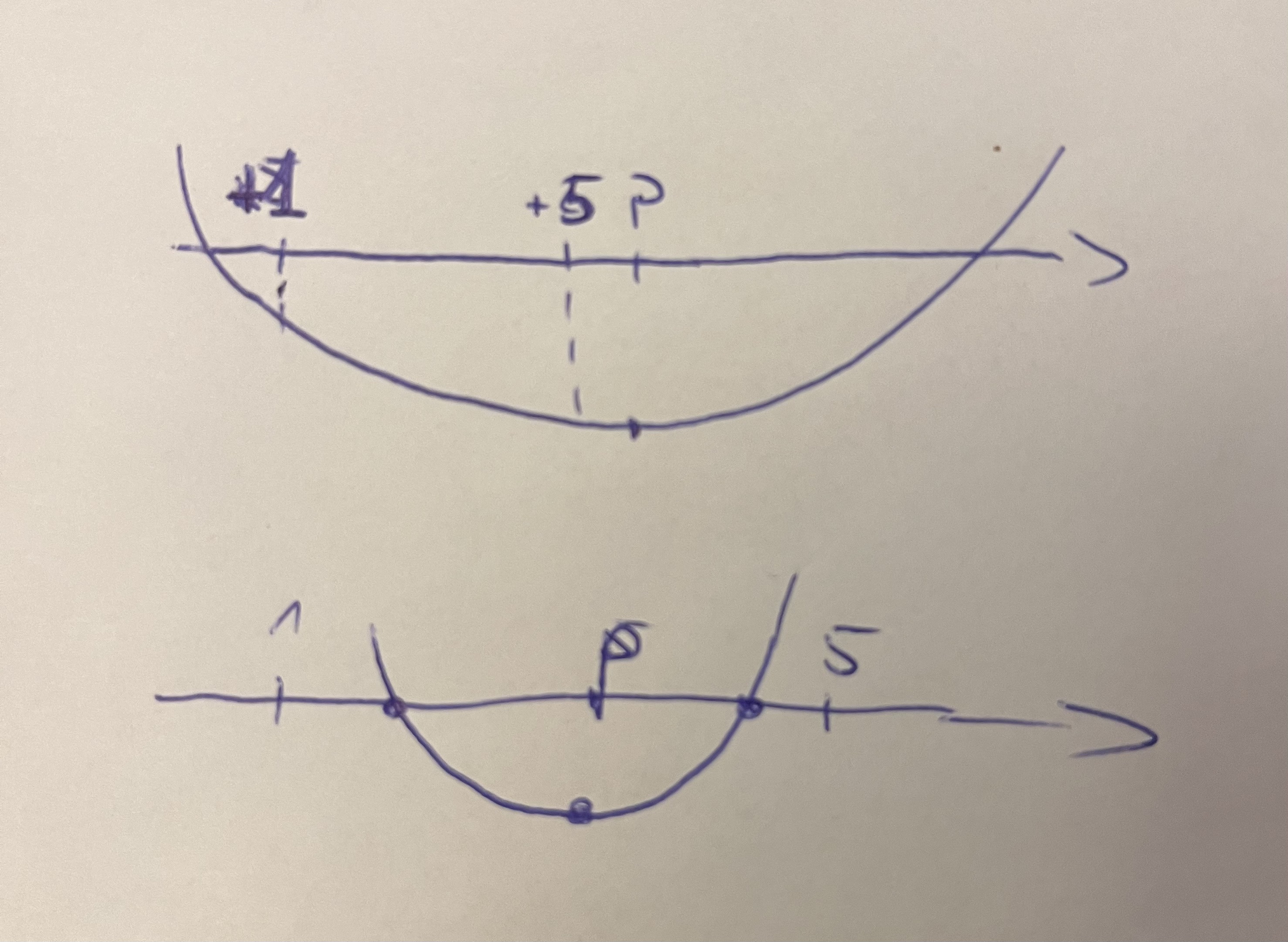
To u góry jest w przypadku gdy chcemy by dla każdego x z <1; 5> f(x) < 0.

To u dołu jest gdy chcemy by miejsca zerowe były z przedziału <1; 5>.

Zauważ, że tak gdzie jest nierówność p nie musi być pomiędzy. Tam gdzie jest równość musi być pomiędzy.

A no tak. Teraz to ma sens. Dziękuję bardzo :D