Arkusz 15 Zad 8
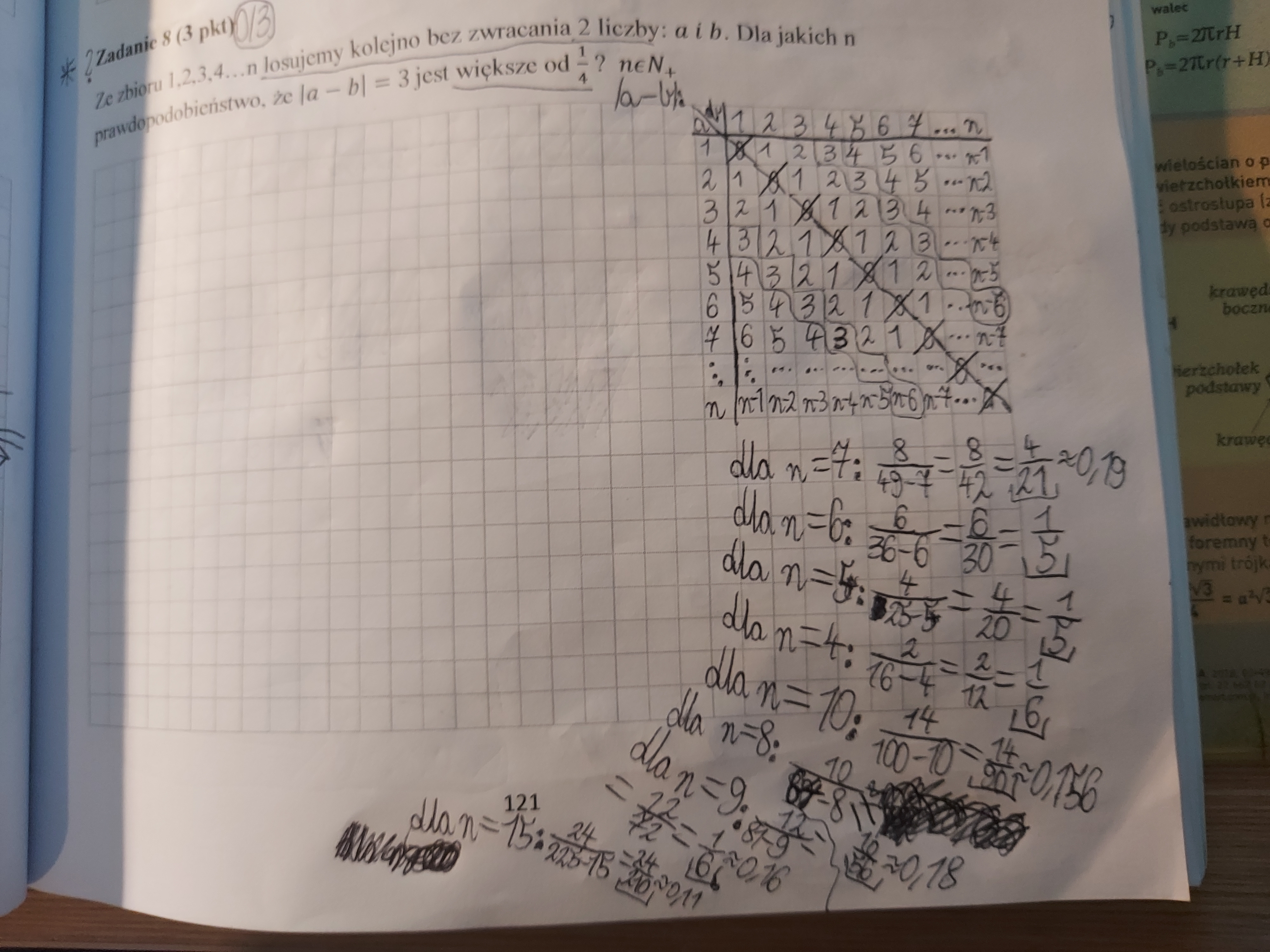
Czy można to rozwiązywać tabelką? Zauważam, że gdy "n" rośnie to prawdopodobieństwo maleje a dla minimalnego n, n=4 jest P=1/5, więc wychodzi na to, że nie ma takiego n, dla którego P>1/4. Natomiast niebardzo rozumiem kryteria w odpowiedziach.
Matematyka prawdopodobieństwo Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli nie można rozwiązywać tego tabelką?
W takim razie o co chodzi w kryteriach? Bo rozumiem jedynie obliczenie omegi bez zwracania.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Liczba sukcesów to 2*(n-3) ponieważ albo jedna liczba musi być mniejsza o 3 od drugiej albo druga liczba musi być mniejsza o 3 od drugiej.
To oznacza, że albo a=b+3, albo b=a+3
W uogólnieniu liczb a, dla których można dobrać b=a+3 jest n-3 (bo a musi być maksymalnie n-3), żeby a+3 <= n) i odwrotnie dla a = b +3 też mamy n-3 takich par.
Czyli łącznie 2* (n-3)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli to wynika z tabelki?
Mi wychodzi od razu, że nie ma takiego n, a w odpowiedziach jest, że 0<n<1.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zgadza się, nie ma takiego "n".
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No tak, ale zauważyłeś to dla kilku "n" - nie dowodzi to temu, że dla każdego "n" tak będzie nawet jeżeli to prawda.