Aksjomat arkusz 10 Zad 17

1) Tak wygląda wykres w geogebrze:

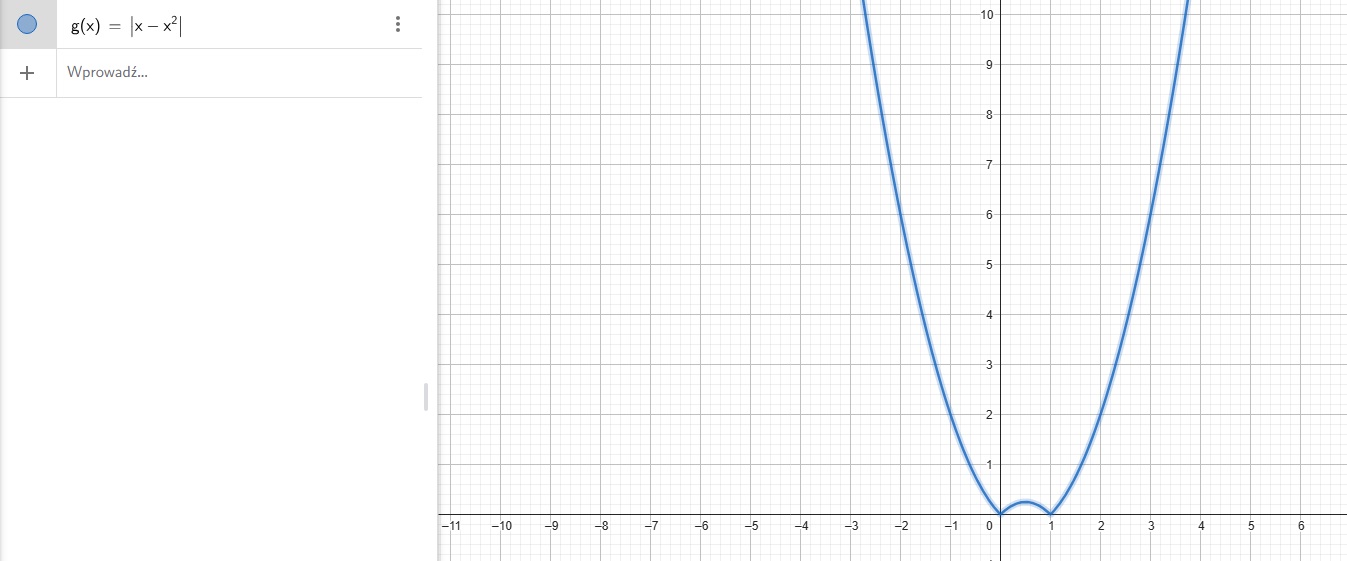
A tak wygląda wykres funkcji f(x)=|x-x^2|

Ponadto dlaczego minimum lokalne=f(0)=0? 

Mógłbyś rozwinąć pytanie ? Widać na wykresie, że jest to minimum lokalne

A jakie przekształcenia wykonać aby narysować wykres f(x)? Bo symetria częściowa mało mi mówi. Równie dobrze poprzez tę symetrię można nałożyć wartość bezwzględną na x^2 (a nie na x). Jak to działa w takim razie?

Chyba nie rozumiem do końca w jakim przedziale bada się minimum lokalne, bo w treści takiego nie określono. Przecież minimum lokalne mogłoby być także na końcu jakiegoś przedziału.

Przecież jest napisane jakie przekształcenie należy wykonać na zdjęcie którym wysłałeś. 

Zapoznaj się z bazą wiedzy: https://szkolamaturzystow.pl/bazawiedzy/przeksztalcenia-wykresu-funkcji

Jest  tam wszystko o przekształceniach wykresów funkcji.

Tzn. na końcu jakiego przedziału ?

Przeczytałem każdy rozdział tego działu, ale dalej nie rozumiem dlaczego tylko x bierzemy w moduł a x^2 już nie. Poza tym czy na maturze obowiązuje jakaś symetria częściowa? Nie ma tam po prostu symetrii względem osi Ox, Oy i początku układu współrzędnych?

No właśnie nie ma podanego takiego przedziału, więc nie wiem na jakiej podstawie możemy określić minimum lokalne, które określa się w podawanym przedziale.

Dlatego nie będzie modułu na x^2 bo właśnie mamy kwadrat który jest zawsze nieujemny.

Tutaj mamy funkcję kwadratową dlatego ekstremum będzie w wierzchołku.

Czyli zawsze żadnej nieujemnej liczby nie bierzemy pod moduł? Gdyby była funkcja np. x-x^3 to wtedy po symetrii względem osi OY byłoby |x-x^3| czy |x|-x^3?

Poza tym czy na maturze obowiązuje jakaś symetria częściowa? Nie ma tam po prostu symetrii względem osi Ox, Oy i początku układu współrzędnych?

W wierzchołku jest maksimum. A minimum lokalne to skąd mamy wiedzieć do jakiego przedziału należy? Bo mogłoby być podane, że dla 1<=x<=2 i wtedy minimum lokalne byłoby dla x=2.

Symetria względem osi OY czyli wykres funkcji y=f(-x) czyli otrzymasz g(x)=x^3-x

Twoje pytanie z minimami lokalnymi jest bardzo specyficzne i nie wiem do czego dążysz - mógłbyś podać przykład konkretnego zadania które jest dla ciebie problematyczne w tej kwestii ? 

A dlaczego nie g(x)=-x^3-x skoro g(x)=f(-x)?

Dalej nie rozumiem dlaczego dla x=0 jest minimum lokalne skoro nie wiemy w jakim przedziale mamy to minimum lokalne wyznaczyć. Gdyby trzeba było wyznaczyć to minimum lokalne dla przedziału, do którego nie należy punkt przegięcia to wtedy minimum lokalne byłoby przecież dla jednego z końca przedziału, w którym tego minima szukamy. Dlatego też uważam, że w tym konkretnym zadaniu powinno być doprecyzowane w jakim przedziale mamy znaleźć to minimum lokalne, bo dla tej funkcji dla D=R tych minimów lokalnych będzie chyba nieskończenie wiele.

No właśnie dlatego, że minus się zniesie. 

W tym zadaniu mamy dokładnie jedno minimum lokalne. 

 0 jest minimum lokalnym, bo spełnia definicję w swojej małej okolicy; nie trzeba wcześniej ustalać konkretnego przedziału.

Czyli ta funkcja x-x³ po SOY będzie |x-x³|? I jest to dlatego, że liczby mogą być ujemne? 

Zatem dla np. x⁴+x²-x po SOY byłoby x⁴+x²-|x| czy x⁴+x²+|-x|?

Załóżmy, że w tym zadaniu przedział, w którym szukamy minimum będzie 1<=x<=2. Czy wtedy nie będzie minimum lokalnego dla x=1?

Pytanie czy mówisz o symetrii klasycznej czy częściowej.

Artur czym dla ciebie jest minimum lokalne ? 

Właśnie niebardzo rozumiem różnicę między symetrią częściową a całkowitą względem dowolnej osi. 

Dla mnie minimum lokalne jest najmniejszą wartością funkcji w badanym przedziale.

Minimum lokalne wcale nie musi być najmniejsze na całym rozważanym zakresie.

A wyrażenie: "bezpośrednie otoczenie" jest umowne?

A dla np. x⁴+x²-x po SOY byłoby x⁴+x²-|x| czy x⁴+x²+|-x|? Jak będzie dla symetrii klasycznej a jak dla częściowej?

Co masz na myśli mówiąc "umowne" ?
Symetria częściowa nie obowiązuje na maturze więc skup się na SOY.

Co to znaczy "bezpośrednie otoczenie"? +/-1 kratka?

To jak wyglądałaby taka funkcja x⁴+x²-x po SOY? W ten sposób: x⁴+x²-|x|?

x^4+x^2+x 
Zapoznaj się artur z bazą wiedzy - tam jest wszystko opisane. Skoro zadajesz takie pytanie świadczy to o tym, że nie do końca zaznajomiłeś się z tym co tam jest. 
Nie można powiedzieć o bezpośrednim otoczeniu, że jest to konkretnie jedna/dwie kratki. To zbieganie wartości.

x^4+x^2+x 
Zapoznaj się artur z bazą wiedzy - tam jest wszystko opisane. Skoro zadajesz takie pytanie świadczy to o tym, że nie do końca zaznajomiłeś się z tym co tam jest. 
Nie można powiedzieć o bezpośrednim otoczeniu, że jest to konkretnie jedna/dwie kratki. To zbieganie wartości.

A czy na maturze może być jednak rysowanie funkcji?

Należy to umieć.