Arkusz 14 Zad 10

Czy to rozwiązanie jest prawidłowe? Bo odpowiedź się zgadza.
Matematyka prawdopodobieństwo Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zastanawia mnie fakt, że rzeczywiście liczby 16, 32, 56, 72, 96 są podzielne przez 8, ale ja nie brałem właściwie pod uwagę cyfry setek (np: 116 nie jest podz przez 8 a 216 jest). Jakim prawem w takim razie to rozwiązanie wyszło dobrze?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ponieważ zliczyłeś wszystkie przypadki - którego przypadku twoim zdaniem brakuje?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Na przykład w 1. przypadku - ostatnie dwie cyfry to 1 i 6 wyszło mi 7*7*6=294 i jest to liczba różnych liczb kończących się na 16 mających różne cyfry, wśród nich jest np. 316, która jest niepodzielna przez 8. Analogicznie w innych przypadkach. Jakim prawem w ten sposób wyszedł mi poprawny wynik?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale mówimy o liczbach pięciocyfrowych.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No tak, wszystko się zgadza. Dalej jest taka rozbieżność jak napisałem w poprzednim komentarzu.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli jaką w końcu pięciocyfrową liczbę zliczyłeś która nie jest podzielna ? Podaj konkretnie tę liczbę.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Z pierwszego przypadku np 52316.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Trochę z przypadku wyszedł ci poprawny wynik - w praktyce powinno to być rozdzielone na różne końcówki:
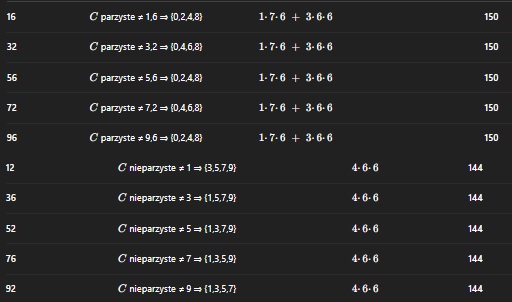
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A co to znaczy C? Całkowite czy cyfra setek?
I czy mógłby Pan wytłumaczyć co symbolizują kolejne czynniki tych iloczynów, które liczymy (chodzi o liczbę sposobów)?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
C to cyfra setek, symbolizują liczbę sposobów
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A wytłumaczyłby Pan kolejne czynniki chociażby na przykładzie 16 na końcu?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Liczba 5 cyfrowa: A B C 1 6
1*7*6=42
1 - jedyny wybór cyfry C (bierzemy 0)
7 - wybór cyfry A spośród 7 dozwolonych
6- wybór cyfry B spośród 6 pozostałych
3*6*6=108
C należy do {2, 4, 8}
3 - tyle pasujących niezerowych parzystych cfyr dla C
6- możliwe cyfry A po wykluczeniu C, 1, 6
6 - możliwe cyfry B po wybraniu A
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jest ok :)