Arkusz 4 Zad 3
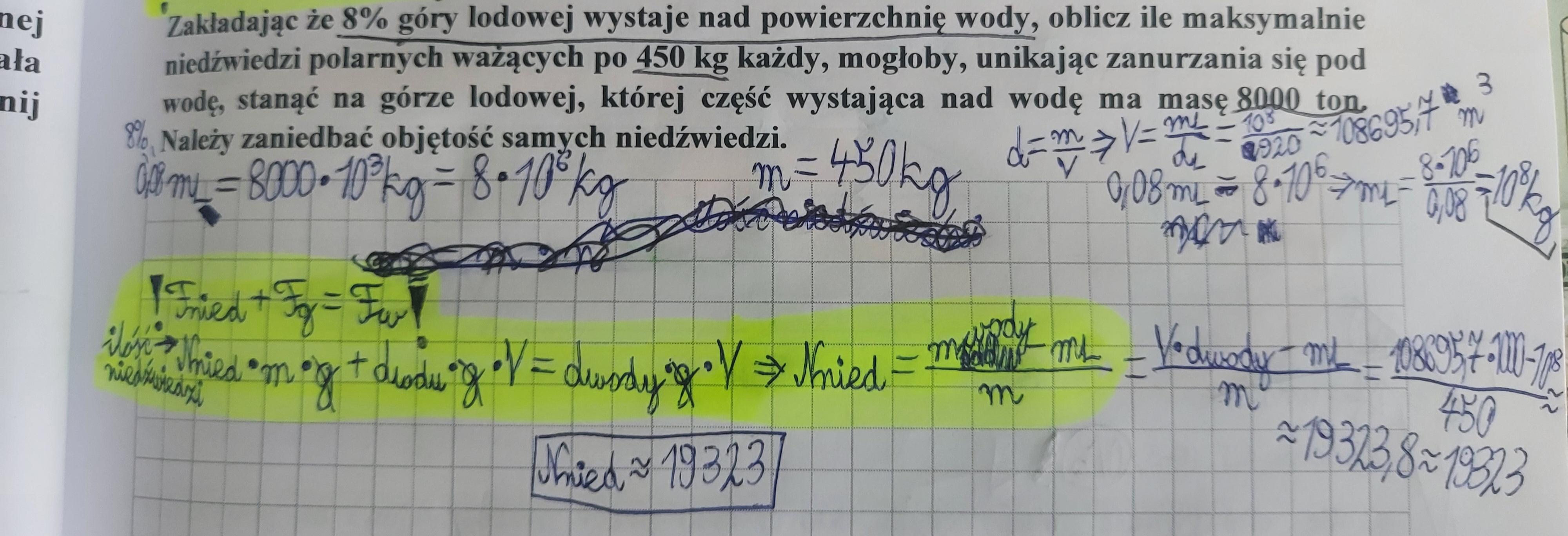

3.2: Nie rozumiem tego przejścia na zaznaczonego na żółto. Skąd wiemy, że d_wody*V_lodu=m_wody?
3.3: 1 - Czy nie jest tak, że cząsteczki w ciałach stałych są najbardziej "ściśnięte"?
3 - Na dnie jest woda o największej gęstości? Dlatego nie zamarza?
Fizyka hydrostatyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.2: Dalej jakoś nie rozumiem jaki to ma związek.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
m_wody to wg przyjętych oznaczeń masa wody wypartej przez całą zanurzoną w tej wodzie górę lodową. Analogia: masz szklankę wody i wrzucasz do niej klocek, który całkowicie się w niej zanurza - w efekcie poziom wody w szklance się podnosi. To o ile zwiększy się objętość całości jest jednocześnie objętością wypartej wody, czyli jednocześnie objętością zanurzonego klocka. Tu naszym "klockiem" jest góra lodowa ;) Czyli m_wody to będzie (zgodnie ze wzorem na objętość) iloczyn gęstości wody i objętości tej wypartej wody. Objętość wypartej wody to objętość góry lodowej. Czyli m_wody = gęstość wody * objętość góry lodowej.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli V_wody_wypartej=V_lodu wynika z prawa Archimedesa?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.2: Bo to jest przypadek graniczny, w którym cała góra lodowa jest już zanurzona, więc V to jest tutaj jednocześnie objętość całej zanurzonej góry lodowej, jak i objętość wypartej w ten sposób wody.
3.3: Dla większości ciał tak w istocie jest, ale woda jest pod tym względem właśnie bardzo nietypowa - lód ma większą objętość niż woda w postaci ciekłej o takiej samej masie (stąd np. rozsadzanie rur, w których zamarznie woda, rozsadzanie skał przez zamarzniętą wodę itp.), więc dla niej jest na odwrót.
Dokładnie - ciała o większej gęstości opadają na dno - dlatego przy dnie będzie woda o temp. ok. 4 stopni Celsjusza, bo w takiej temp. woda ma największą gęstość. No i ona tam nie zamarznie.