Arkusz 5 Zad 3
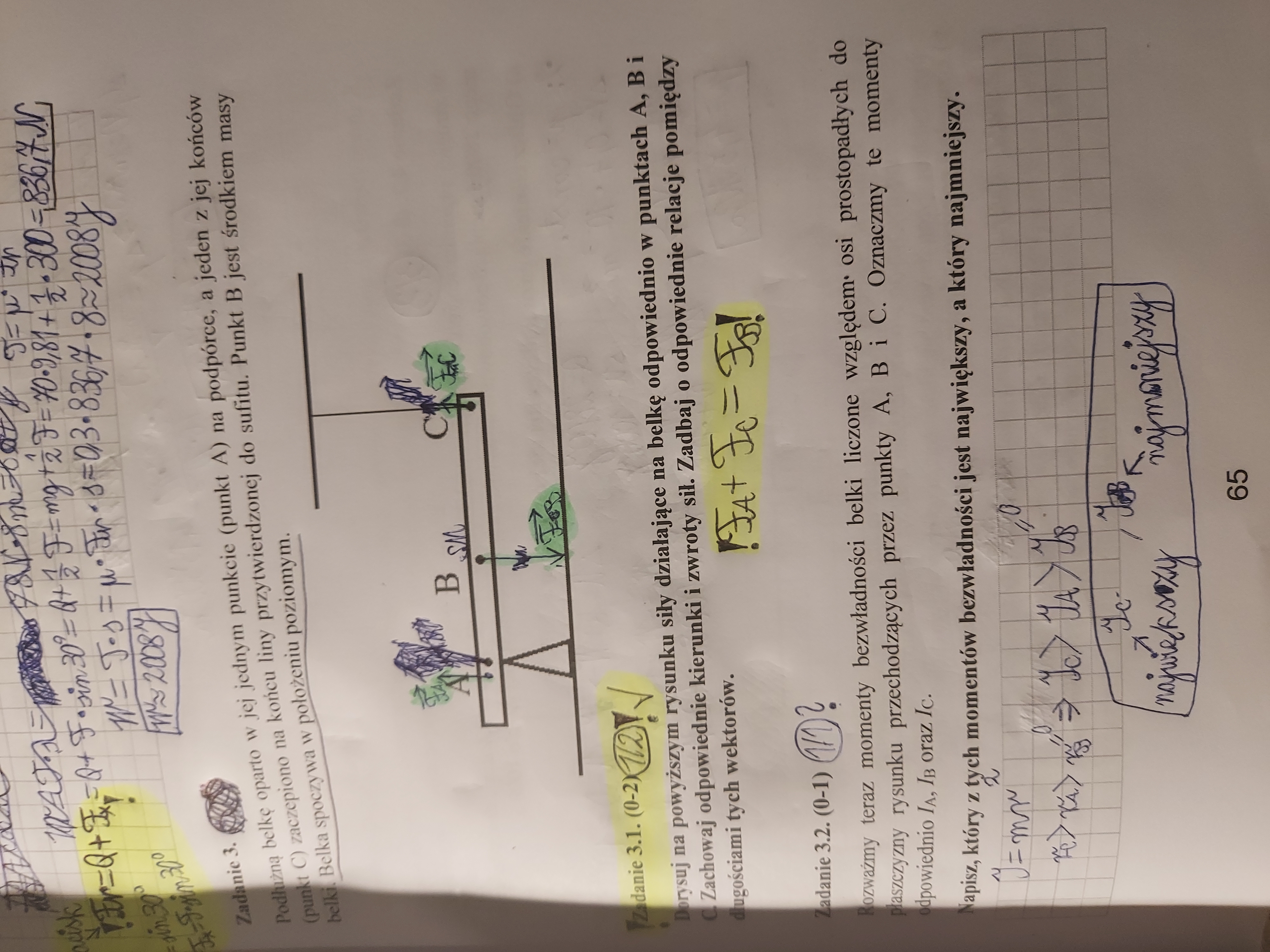
3.1: Skąd wiemy, że F_a>F_c?
3.2: Czy należy to rozpatrywać względem osi przechodzącej przez punkt B? Bo w sumie nie do końca wiadomo.
Fizyka bryła sztywna Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1: A fakt, że F_a jest zwrócone w górę jest spowodowany przez 1ZDN: F_b=F_a+F_c?
3.2: Czyli tutaj I_b=0?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1: Można to z tego wywnioskować, ale tak naprawdę to od razu wynika to z faktu, że belka jest w punkcie A podparta przez podpórkę. A więc belka działa na podpórkę w dół, więc zgodnie z III ZDN podpórka musi "oddawać" belce z siłą zwróconą w górę.
3.2: Nie, I_b nie jest zerowe, ale jest najmniejsze ze wszystkich.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.2: Ale przecież punkt B jest w geometrycznym środku belki.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No tak, ale to nie znaczy, że moment bezwładności belki względem jej środka jest zerowy. Zgodnie z definicją momentu bezwładności jest to suma wyrażeń m_i*r_i^2, gdzie m_i to masa i-tego punktu wchodzącego w skład bryły, a r_i to odległość tego punktu od osi obrotu. W belce mamy zdecydowanie punkty, których r_i jest większe od zera jeśli liczymy tę odległość od punktu B.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No to ja to rozumiem teraz tak:
- Oś a: Icałk=m_b*r_ab+m_c*r_ac
- Oś b: Icałk=m_a*r_ab+m_c*r_bc
- Oś c: Icałk=m_a*r_ac+m_b*r_bc
Oraz r_ab<r_bc<r_ac
Czy to jest poprawne?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Hmm, nie bardzo wiem czym jest m_a, m_b itd. Poza tym odległości r powinny być do kwadratu, ale to już szczegół. Ale chodzi o to, że ciężko tu dokładnie zsumować wszystkie te punkty, bo w praktyce jest ich bardzo wiele. Można sobie bowiem wyobrazić to tak, że cała belka składa się z tych bardzo wielu punktów, z których każdy ma taką samą masę m. I teraz w zależności od tego, względem której osi będziemy liczyli ten moment bezwładności, to odległości tych punktów (czyli te wartości r, a co za tym idzie ich kwadraty r^2) od tej osi będą się różniły. Jeśli obierzemy oś przechodzącą przez punkt B, to te kwadraty odległości średnio będą najmniejsze, jeśli zaś obierzemy ją w punkcie C, to będą one największe. Stąd Ib < Ia < Ic.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli po prostu największa część masy jest:
- najdalej od punktu C => I_c=Imax
- najbliżej punktu B => I_b=Imin
Czy można to tak tłumaczyć?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1: Wszystkim rządzi tutaj równowaga momentów sił - względem dowolnego punktu momenty sił działających na belkę muszą się równoważyć. I tak, np. rozpatrując te momenty względem punktu A (wtedy moment siły Fa jest zerowy, bo ramię tej siły jest zerowe), widzimy, że siła Fb musi być większa niż Fc, bo ramię siły Fb jest mniejsze niż ramię siły Fc. Z tego samego powodu rozpatrując momenty względem punktu B, dochodzimy do wniosku, że Fc < Fa, bo w tym przypadku ramię siły Fc jest dłuższe niż ramię siły Fa.
3.2: Zgodnie z treścią rozpatrujemy momenty bezwładności względem trzech różnych osi - jednej przechodzącej przez punkt A, drugiej przez punkt B, a trzeciej przez punkt C. W tych trzech przypadkach otrzymujemy trzy różne momenty bezwładności Ia, Ib i Ic, i musimy stwierdzić, który z nich jest najmniejszy, a który największy. I wynika to wprost z definicji momentu bezwładności, które (parafrazując) mówi, że im większa część masy znajduje się dalej od rozpatrywanej osi, tym większy jest moment bezwładności= liczony względem tej osi.