Arkusz 22 Zad 1

Dlaczego trzeba w tym zadaniu rozpatrywać przypadek q=0 skoro ewidentnie wychodzi, że q=-1/2?
Matematyka szeregi Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
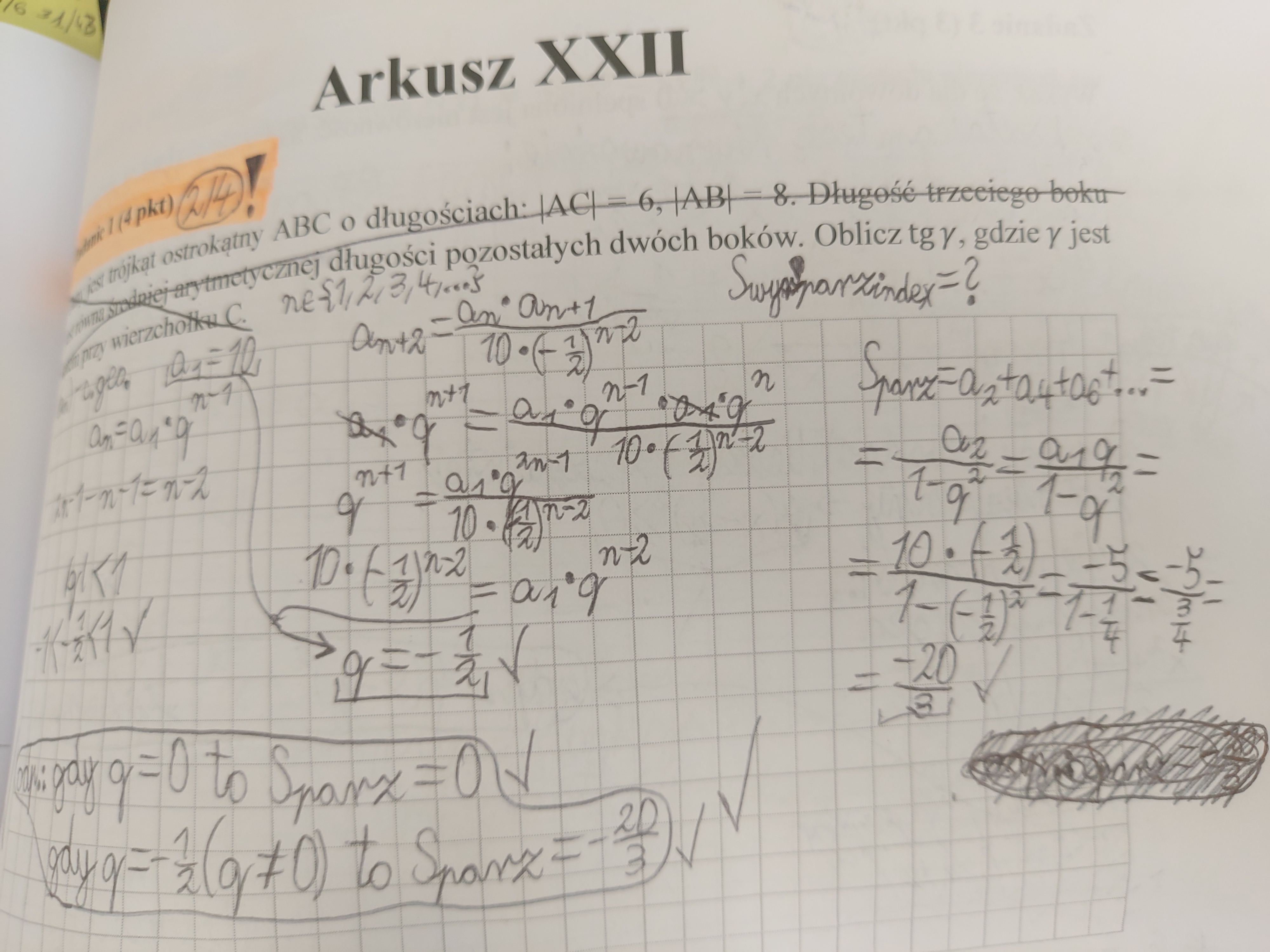
Ja tu właściwie nigdzie nie dzieliłem przez 1^(n-2).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale rozważyłeś przypadek q=0
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale to już dopisałem po sprawdzeniu odpowiedzi. Nie wiem dlaczego ten przypadek q=0 musi istnieć skoro nigdzie nie dzieliłem przez nic sprzecznego.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
On po prostu istnieje, musimy go rozważyć osobno bo dla q=0 wyrażenia typu q^(-1), q^(2-n) nie mają sensu. Gdy q=0 to ciąg geometryczny istnieje i spełnia rekurencję, ale wszystkie wyrazy od n>=2 są zerami. Stad przypadek q=0 nie może zostać uzyskany z poprzednich przekształceń i trzeba go potraktować oddzielnie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A gdyby tutaj nie było ciągu rekurencyjnego tylko po prostu ciąg geometryczny to musielibyśmy rozpatrywać ten przypadek q=0?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Podaj konkretny przykład zadania.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Np. po prostu an=a1*q^(n-1).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tzn. chciałbyś wyrzucić całą część z rekurencyjnością ? Zapisz to polecenie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
"Rozważmy c.geo., którego a1=10. Wyznacz sumę wyrazów o parzystych indeksach tego ciągu." Czy wtedy też rozpatrujemy przypadek q=0?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Należy rozważyć ten przypadek ponieważ w wyprowadzeniu, w którym dzielimy przez 1^(n-2) albo przyjmujemy, że funkcja potęgowa jest odwracalna, ukryte jest założenie q != 0