Arkusz 22 Zad 2
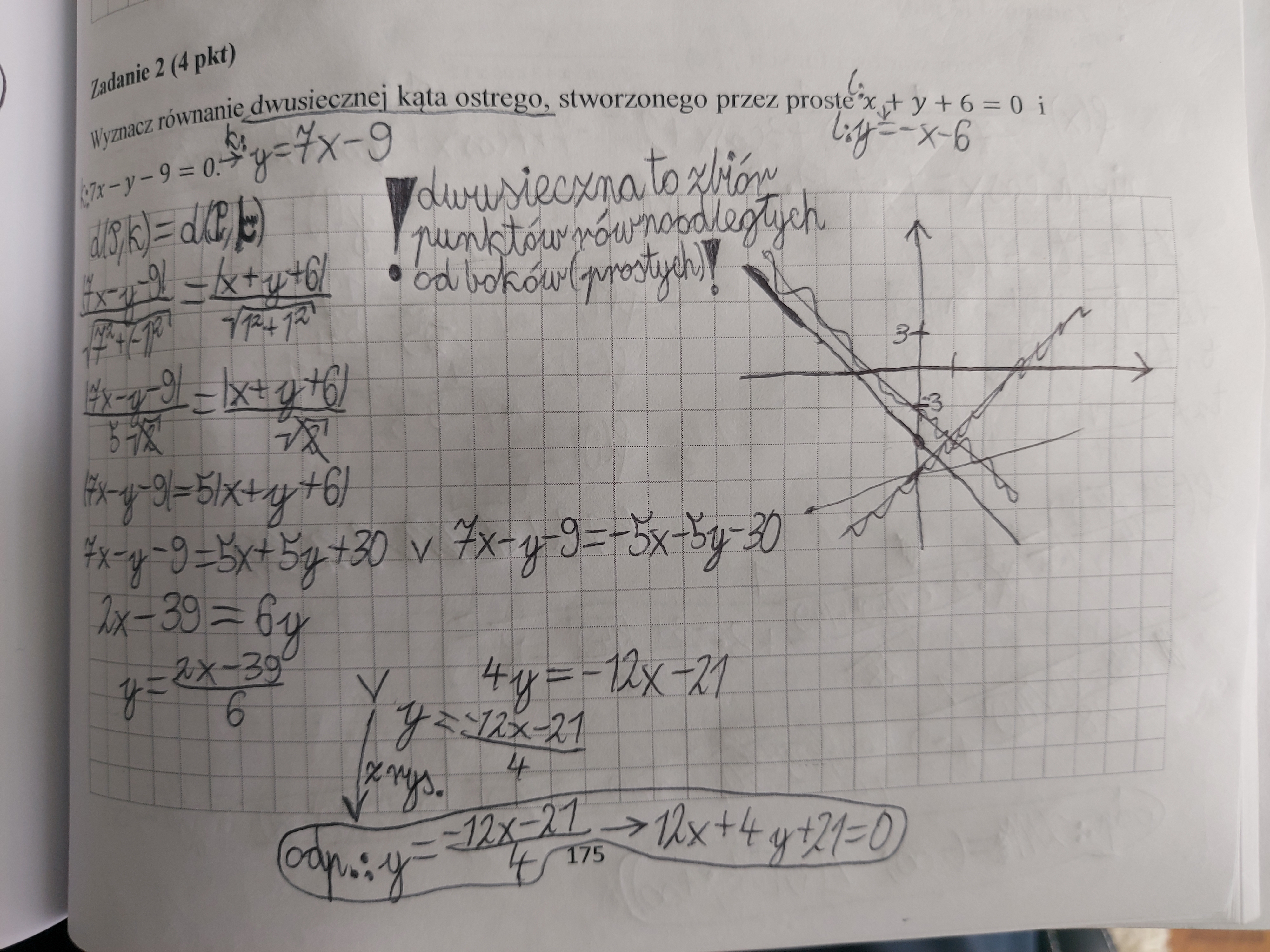
Na lekcji apropo podobnego zadania mówił Pan, że nie można odczytać z rysunku ostatecznej dwusiecznej, a nawet w odpowiedziach jest napisane, żeby tak zrobić.
Jak inaczej stwierdzić, która dwusieczna jest prawidłowa dla kąta ostrego?
Matematyka geometria analityczna Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy Pan wysłał jakiś plik w ostatniej wiadomości? Bo tak to wygląda, ale nic się nie otwiera.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Teraz widać? Był to rysunek, nie jest on potrzebny do zrozumienia, ale może trochę rozjaśni.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, widać rysunek, ale nie rozumiem gdzie jest punkt S i po co używać tutaj wektorów? "Wybierasz dowolne wektory v, w, takie, że v równoległe do jednej dwusiecznej, w równoległe do drugiej dwusiecznej, następnie obliczasz v' = v/|v|, w' = w/|w|, w ten sposób oba wektory będą miały długość 1" <-skąd to wiemy o długości wektorów?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Punkt S to ten punkt przecięcia prostych na rysunku, zauważ, że chcemy |AS| = |BS|.
Jeśli nie chcesz wektorów to możesz wybrać dowolny punkt A na jednej prostej, obliczyć długość |AS| i wybrać na drugiej prostej taki punkt B by |BS|=|AB| (można zastosować wzór na długość odcinka ) i B leży na prostej, z układu równań powinny wyjść współrzędne punktu B. Istnieje w tej metodzie niebezpiecześstwo wystąpienia brzydkich wyników.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli ja mam sobie losowo wybrać punkt A? I potem z tego, że SA jest prostopadłe do SB obliczyć punkt B?
"Tu mogą wyjść brzydkie wyniki" <- a w metodzie z wektorami już nie?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak.
Z wektorami też mogą wychodzić brzydkie wyniki.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A mógłby Pan pokazać chociaż początek tego sprawdzenia w tym konkretnym zadaniu? Bo chyba jednak nie do końca to rozumiem.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W sumie to może jest jeszcze łatwiejsza opcja:

Wylicz cosinus kąta pomiędzy jedną dwusieczną a dowolną prosta, oraz drugą dwusieczną a dowolną prostą, następnie oszacuj który kąt jest mniejszy.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A skąd się biorą te wzory? Bo raczej tego nie zapamiętam na maturze.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wykazywanie takich wzorów to już nie trudne zadanie, ale dopiero na poziomie studiów.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To pokazałby Pan początek sprawdzenia jaki sposób stwierdzić, która dwusieczna jest tą właściwą bazując na naszych maturalnych możliwościach? Dalej nie do końca to rozumiem.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
S to punkt przecięcia prostych.
Masz tutaj początek metody z wektorami:

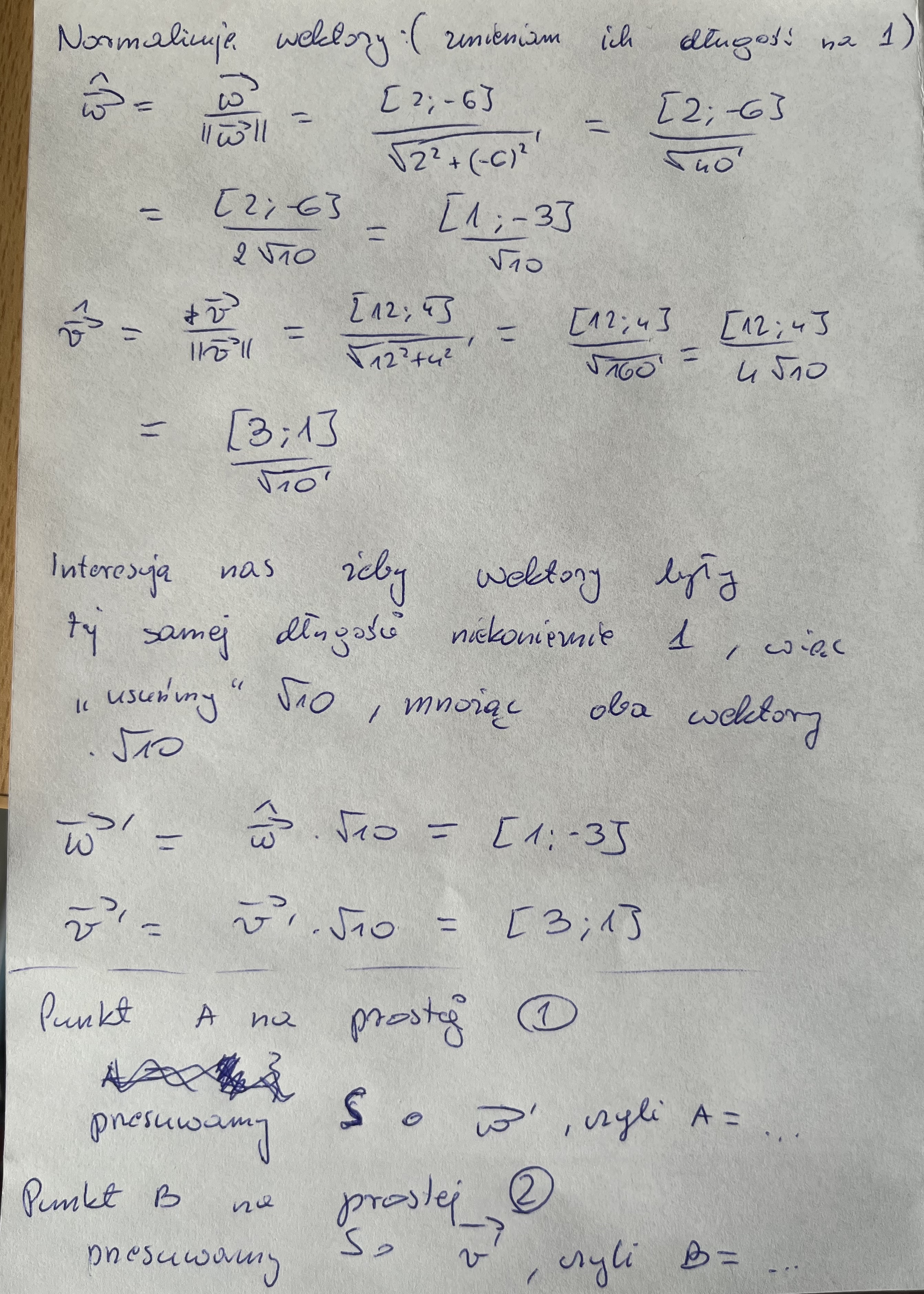
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Skąd wiemy jak zapisac wektory prostopadłe do prostej? Z tego co widzę nie ma tego w kw.
2: Dlaczego chcemy "normalizować" wektory i o co z tym chodzi?
3: Czy myśli Pan, że na maturze może się coś takiego trafić, gdzie właśnie samo to rozumowanie będzie za 1 punkt? Jak rozumiem tak było w kryteriach w tym zadaniu.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. Patrz na to co wysłałem kilka postów wcześniej w zielonej ramce, tam jest na początku wytłumaczone.
2. Normalizowanie wektorów to dzielenie wektora przez jego długość, dzięki temu wektor osiąga długość 1, a nas interesują wektory takiej samej długości.
3. Tak.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A skoro na zajęciach nie było pokazane tego typu obliczenie to czy szansa, że ono się pojawi jest niska?
Jak działa iloczyn skalarny w matematyce? Nie mogę tego znaleźć w bazie wiedzy. Czy to nie jest wymagane na maturę?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. Tak.
2. Iloczyn skalarny jest na poziomie studiów, nie jest potrzebny na maturze.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A czy prostopadłość wektorów do prostej albo wektorów wzajemnie do siebie jest wymagana na maturze?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Może się przydać, warto to wiedzieć
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To czy da się w takim razie te wzory z czymś skojarzyć jeśli nie ma ich w karcie wzorów?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jedynie możesz skojarzyć, że pierwiastek z A1^2 + B1^2 to długość wektora [A1; B1].
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A jak wtedy jeszcze raz zapisać prostopadłość wektora do prostej?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Prostopadłość wektora do prostej zapisujemy tak jak prostopadłość prostej do prostej, czyli dla wektora v i prostej l:
v ⊥ l
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chodziło mi bardziej o współczynniki.
1: Czy dobrze rozumiem, że jak wektor jest prostopadły do prostej to ma takie współrzędne jak jej współczynniki?
2: Jak taka relacja wygląda, gdy wektor jest równoległy do prostej?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. Tak jak pisałem i było w tekście który wysyłałem: tak wektor prostopadły do prostej Ax+By+C= 0, ma współrzędne [A, B].
2. Wektor [f;g] jest równoległy do prostej Ax + By + C = 0, wtedy i tylko wtedy gdy: f*A + g*B = 0.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zauważ, że jeśli wybierzesz punkty A i B każdy na innej dwusiecznej, w TEJ SAMEJ odległości od przecięcia prostych (nazwijmy ten punkt S), to ten punkt który znajduje się bliżej którejkolwiek z prostych jest na szukanej dwusiecznej.
Punkty takie możesz wybrać np w taki sposób:
Wybierasz dowolne wektory v, w, takie, że v równoległe do jednej dwusiecznej, w równoległe do drugiej dwusiecznej, następnie obliczasz v' = v/|v|, w' = w/|w|, w ten sposób oba wektory będą miały długość 1. Następnie przesuwając S o v' otrzymujesz A, a przesuwając S o w' dostajesz B.