Arkusz 22 Zad 6
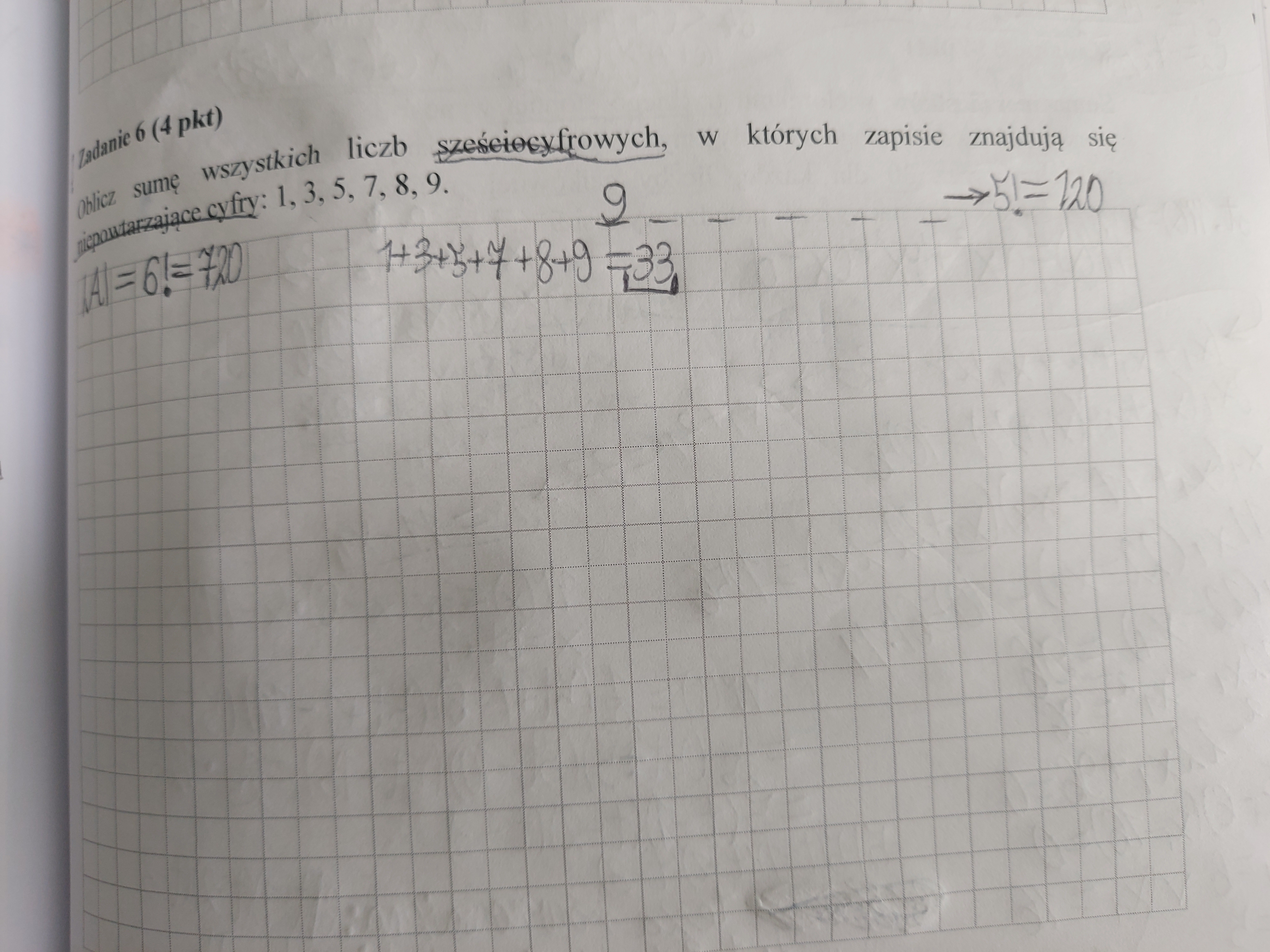

Nie rozumiem dlaczego 33 należy przemnożyć przez 5! I dlaczego ta suma tak wygląda w kryterium za 3 punkty?
Matematyka kombinatoryka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jak to każda występuje 5! razy? Chodzi o każdą sumę równą 33? Niebardzo to rozumiem.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tzn. każda z cyfr pojawi się dokładnie w 5! liczb jako cyfra np. jedności, dziesiątek itd.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ale to jeszcze jakoś chyba trzeba tutaj użyć faktu, że takich liczb istnieje ogólnie 6!=720. Więc jeśli już to raczej mnożyłbym przez 6! a nie przez 5!
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur wydaje mi się, że z tym 5! chodzi o to, że w momencie, gdy obstawisz np liczbę 7 na miejsce jedności to pozostaje ci pięć liczb na pięć pozostałych miejsc stad 5!
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale na cyfrę jedności można wybrać 6 cyfr, więc liczba tych sposobów moim zdaniem to 6!
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ale jak pisałem wyżej liczbę jedności można jeszcze wybrać na 6 sposobów.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur - chodzi o zamianę miejsc:

- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Bo suma cyfr w jednym miejscu na jednej pozycji to:
1+3+5+7+8+9=33
Ponieważ każda z nich występuje 5! razy, łączna suma cyfr w danym miejscu wynosi 33*5!