[Zadanie domowe 20] zad 5 (wektory??)
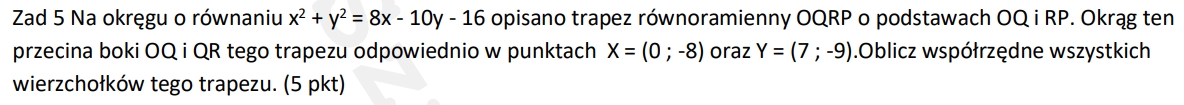
Czy te zadanie można wykonać wektorami?
Kroki działania:
- wyznaczam proste przechodzące przez (1 prosta) pkt. X (2 prosta) pkt. Y, ktore sa odleglo od S o r
- wyznaczam pkt. przeciecia tych prostych i dostaje pkt Q
- wyznaczam wektor XQ i przesuam X o -XQ otrzymujac pkt. O
- wyznaczam wektor XS i przesuwam pkt. X o 2*XS dostajac srodek podstawy PR - Z
i teraz pojawia sie dylemat, ktora opcja jest poprawna - obie daja ta sama odpowiedz:
- wyznaczam wektor SY i przesuwam Z o SY i -SY dostajac P i R
albo
- znajduje rownanie prostej PR i przyrownuje do prostej QR otrzymujac pkt. R
- tworze wektor ZR i przesuwam Z o -ZR otrzymujac pkt. P
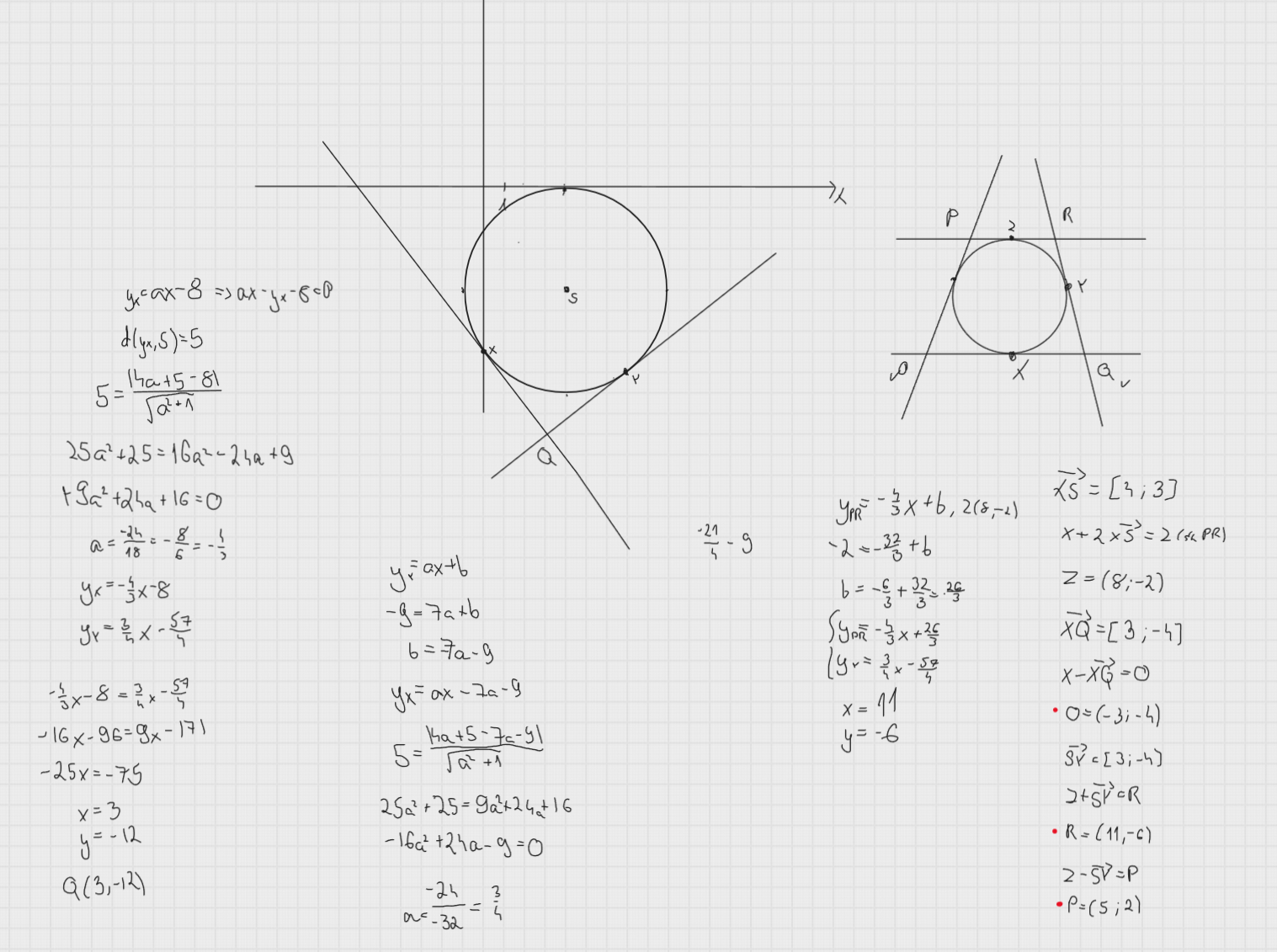
Pytania:
- czy podana wyzej logika jest poprawna
- czy mozna zalozyc, ze Z+SY=R? (czyli, ktora opcja odnalezenia pkt. R rozpisana wyzej jest poprawna)
- mozna tylko zalozyc ze pkt. X i Z dzieli proste na pol?
- czy ze wzgledu na to ze ten trapez jest rownoramienny QY=O(pkt. stycznosci pod pkt. P)?
- jakie ew. mozna dac zalozenia do tych bokow podanych wyzej
geom. anal. Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. Logika nr 2 poprawna, logika nr 1 nie poprawna.
2. Nie, zauważ, że wektor SY nie jest równoległy do podstaw (chyba, że ten trapez jest prostokątem) więc po przesunięciu Z o wektor SY, otrzymany punkt Z' "wypada" z prostej zawierającej podstawę.
3. Tak te punkty dzielą odcinki na pół, zapisz to w swoim rozwiązaniu zanim przystąpisz do obliczania Z.
4. Nie, spójrz znowu na kierunek wektorów, są całkowicie inne, ale długości ich będą takie same.
5. Nie rozumiem o jakie założenia ci chodzi. Na pewno założenie z logiki nr 1 jest niepoprawne.