Artur 34 wyśw.
19-04-2025 18:03
Nowa era arkusz 1 Zad 16
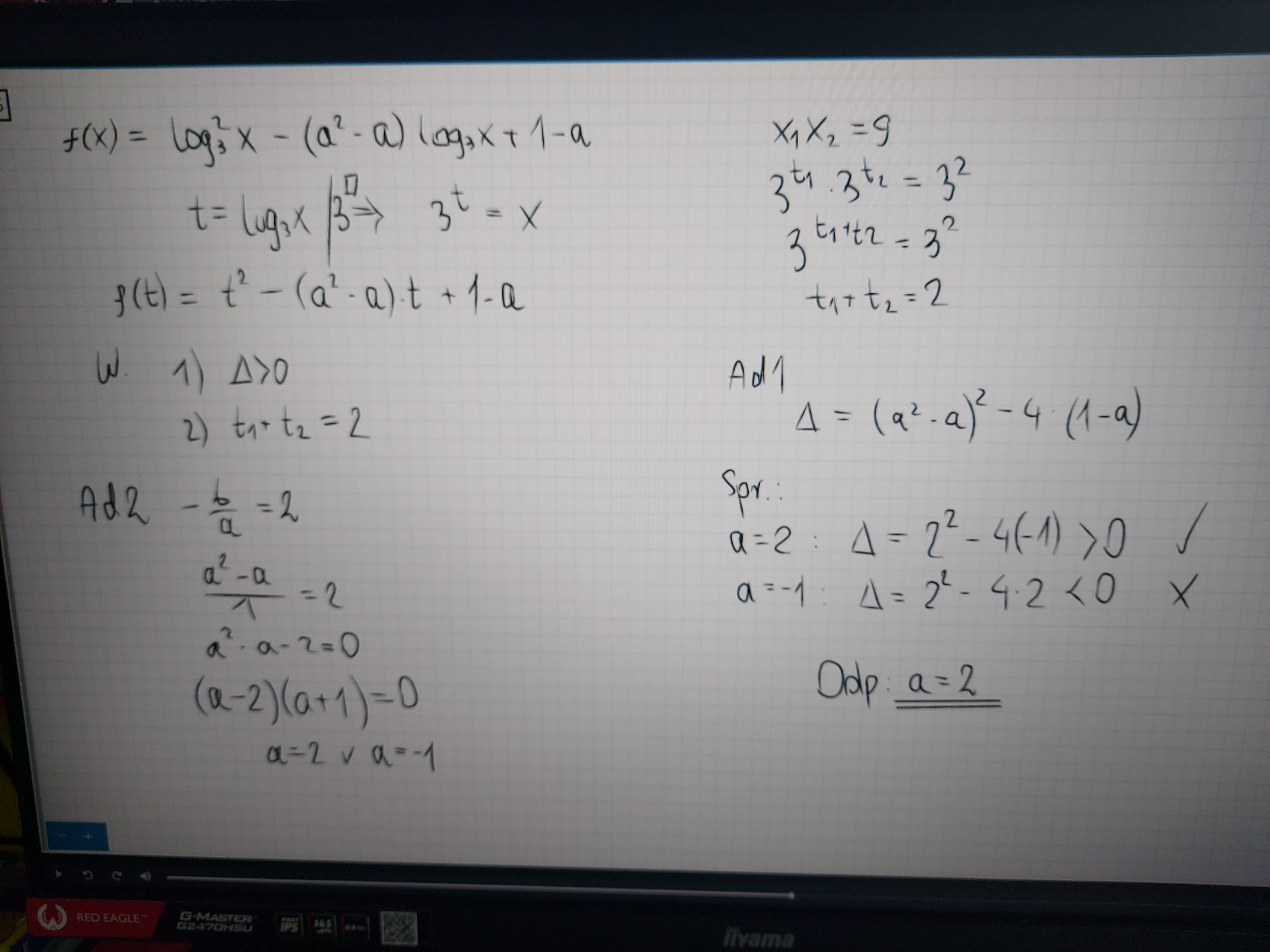
Co jeśli po prawej w postawie byłoby "-3"? Przecież zachodzi także równość: (-3)^2=9 (niebieskie podkreślenie).
Czyli jeśli jednym z warunków funkcji kwadratowej jest równanie to zawsze można tylko je rozwiązać i sprawdzać dla wartości uzyskanych w tym równaniu pozostałe warunki i to daje także maksymalną ilość punktów tak?
Matematyka funkcja kwadratowa Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski
23-04-2025 01:04
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1.
No dobrze załóżmy, że masz 3^(t1 + t2) = (-3)^2, to po prostu przekształcasz to do postaci: 3^(t1 + t2) = (-3)^2 = 3^2, czyli: 3^(t1 + t2) = 3^2, czyli to samo.
Nie ma sensu szukać dziury w całym, po prostu jeśli masz x^2, to możesz jeśli ci łatwiej zapisać jako (-x)^2, to już zależy od tego co ci łatwiej zrobić, tutaj stosowanie -3 mija się z celem, więc stosujesz -(-3) = 3.
2.
Tak, bardzo dobrze trzeba sobie optymalizować robotę, max punktów dostaniesz ;)