Nowa Era arkusz 8 Zad 11
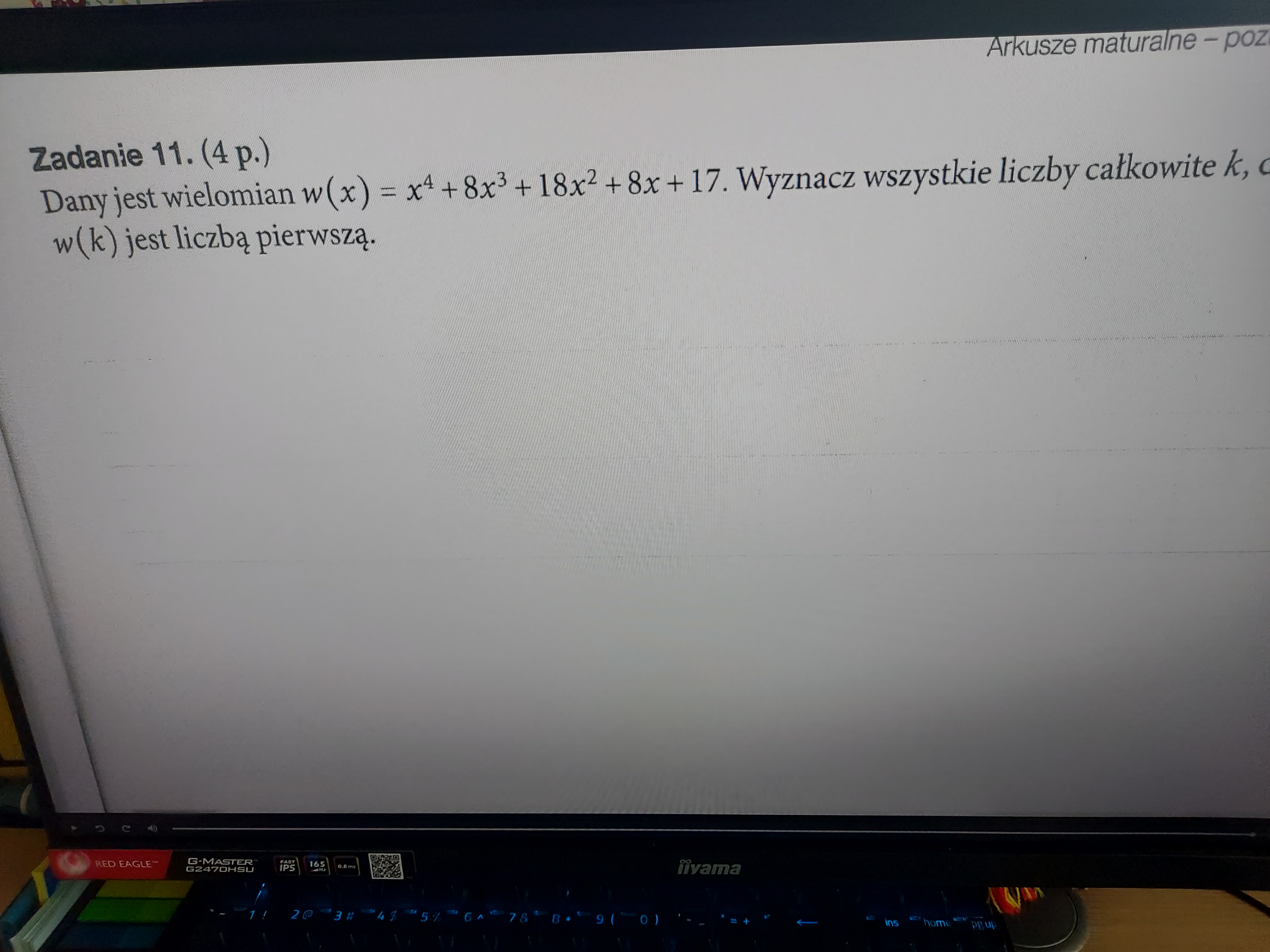

Nie rozumiem tego momentu z przemnażaniem razy 1. Dlaczego należy tak robić i czy zawsze mnożymy razy 1 czy zdarza się, że także przez inne liczby?
Matematyka wielomiany Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tę dalszą część rozumiem, ale dalej nie wiem dlaczego w tej pomarańczowej ramce mnożymy akurat razy 1 aby rozbić te nawiasy? Czy jest to dlatego, że P=1*P lub P=-1*(-P)?
Dlaczego nie przemnożymy tego razy -1?
Czy zawsze w takim przypadku mnożymy to razy 1?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie, to na pomarańczowo nie ma żadnego powiązania z częścią zadania dotyczącą liczb pierwszych, chodzi tylko o kwestie rozbicia wielomianu, a właściwie zauważenia, że jeśli rozbijesz 18x^2 = 17X^2 + 1x^2 to masz takie same współczynniki w lewej i prawej części wielomianu, więc wyciągając x^2 z jednej części, otrzymujesz fajne rozbicie całego wielomianu.
Popatrzymy na inny przypadek z innymi liczbami niż 1 i -1:
5x^4 + x^3 + 7x^2 + x + 2, jeśli rozbijesz 7x^2 = 2x^2 + 5x^2 to otrzymasz: 5x^4 + x^3 + 2x^2 + 5x^2 + x + 2 = x^2 * (5x^2 + x + 2) + 5x^2 + x + 2 = (x^2+1)(5x^2 + x + 2)
Tutaj rozbijasz inaczej, bez żadnej 1, lub -1.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A czy ten wielomian 5x^4 + x^3 + 7x^2 + x + 2 da się rozbić w taki sam sposób jak jest pokazany na nagraniu? Czyli z przemnażaniem?
Czy to działa tylko gdy są 2 wyrazy wspólne? I wtedy zawsze mnoży się razy 1 czy niekoniecznie?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie wiem co masz na myśli.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy wielomian 5x^4 + x^3 + 7x^2 + x + 2 da się rozbić w ten sam sposób jak wielomian x^4 + 8x^3 + 18x^2 + 8x + 17?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Pokaż mi sposób rozbicia w jaki chcesz rozbić x^4 + 8x^3 ..., a ja ci powiem czy ten 5x^4 tak można.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Sposób rozbicia pierwszego z tych wielomianów pokazał Pan na tamtym nagraniu i jest na pierwszym zdjęciu tego posta.
1: Pytanie czy działa on zawsze w ten sposób, że gdy jest np 2n+1 liczb to współczynniki przy 2 oraz 2n ; 3 oraz 2n-1 itd. (aż do środkowego wyrazu są takie same z czegoś innego to wynika?
2: Czy da się tak rozbijać wielomiany gdy ilość tych współczynników jest parzysta?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale ja go rozbiłem w ten sam sposób, tylko bez takiego słupka, ale to jest ta sama metoda.
Tak, możesz wykorzystać taki słupek na pomarańczowo jeśli ci łatwiej.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Pytanie czy ten sposób działa zawsze, że gdy jest np 2n+1 liczb to współczynniki przy 2 oraz 2n ; 3 oraz 2n-1 itd. (aż do środkowego wyrazu są takie same z czegoś innego to wynika?
2: Czy da się tak rozbijać wielomiany gdy ilość tych współczynników jest parzysta?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. Nie, ten sposób działa tylko w specyficznych sytuacjach.
2. Tak, tylko wtedy nie rozbijasz środkowego wyrazu na sumę 2 innych, tylko od razu doszukujesz się zależności.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zauważ, że rozbiliśmy wyrażenie na dwa nawiasy, a podstawiając k całkowite, oba stają się liczbami całkowitymi które mnożysz.
Z definicji liczba pierwsza nie ma dzielników innych niż 1 i ona sama, więc wnioskujemy że skoro nawiasy bedą liczbami całkowitymi to koniecznie któryś z nich musi być wartości 1, a drugi liczba pierwszą, lub pierwszy o wartości -1 a drugi ma być -1*liczba pierwsza. Dlatego później po wyliczeniu k z jednego nawiasu należy sprawdzić czy drugi nawias jest liczbą pierwszą.