MaksymilianMlodawski 24 wyśw. 22-04-2025 20:41

Zad 11 arkusz 21


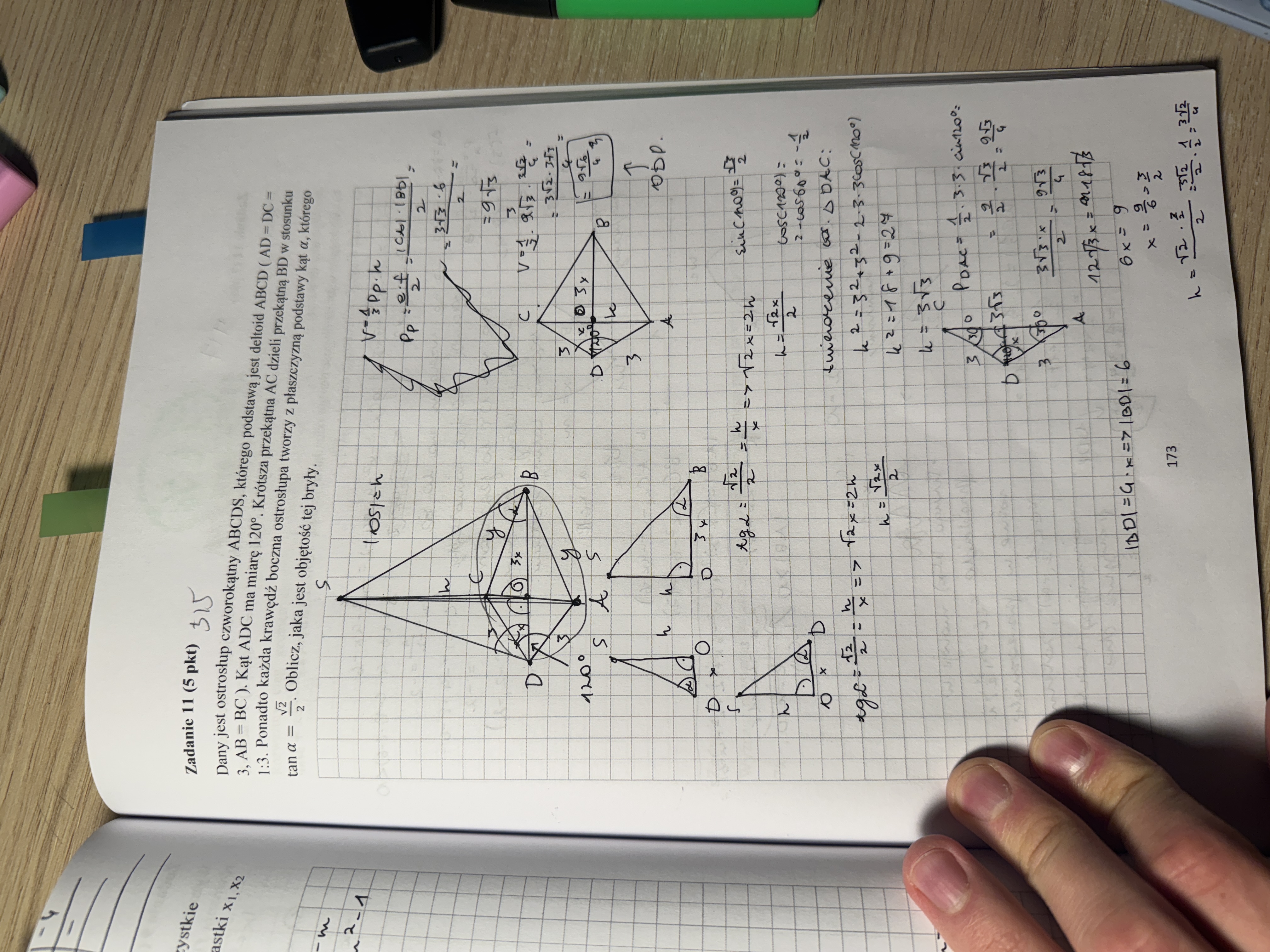
Nie skorzystałem w moim rozwiązaniu z danej że krawędzie tego ostrosłupa są nachylone pod tym samym kątem zatem okrąg opisany na podstawie i jego środek jest spodkiem wysokości ostrosłupa - dlatego że nie jestem pewien czy to w ten sposób działa w czworokącie w podstawie - proszę o wyjaśnienie.

I w takim razie czy wynika z tego wprost że przekątne dzielą się na dwie równe części? 

Ponad to ze względu na to że chyba nie skorzystałem z tej własności wyszedł mi nieco inny wynik bo w obu przypadkach mam 4 zamiast 2 w mianowniku - czy ktoś mógłby zweryfikować, dziękuję z góry. 

Stereometria Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 26-04-2025 18:16

Otóż jeśli zastosujesz twierdzenie to prawda, że spodek będzie środkiem okręgu opisanego na czworokącie (wykaże to potem), lecz to nie znaczy, że spodek jest w punkcie przecięcia przekątnych, będzie gdzie indziej, ALE dużo informacji daje sama wiedza, że na podstawie da się opisać okrąg (patrz: warunek opisania okręgu na czworokącie, który daje informacje o kątach).


Dowód, że jeśli krawędzie boczne padają pod tym samym kątem to spodek wysokości to środek okręgu opisanego na czworokącie: