Arkusz 3 Pazdro Zad 3.1, 6, 9




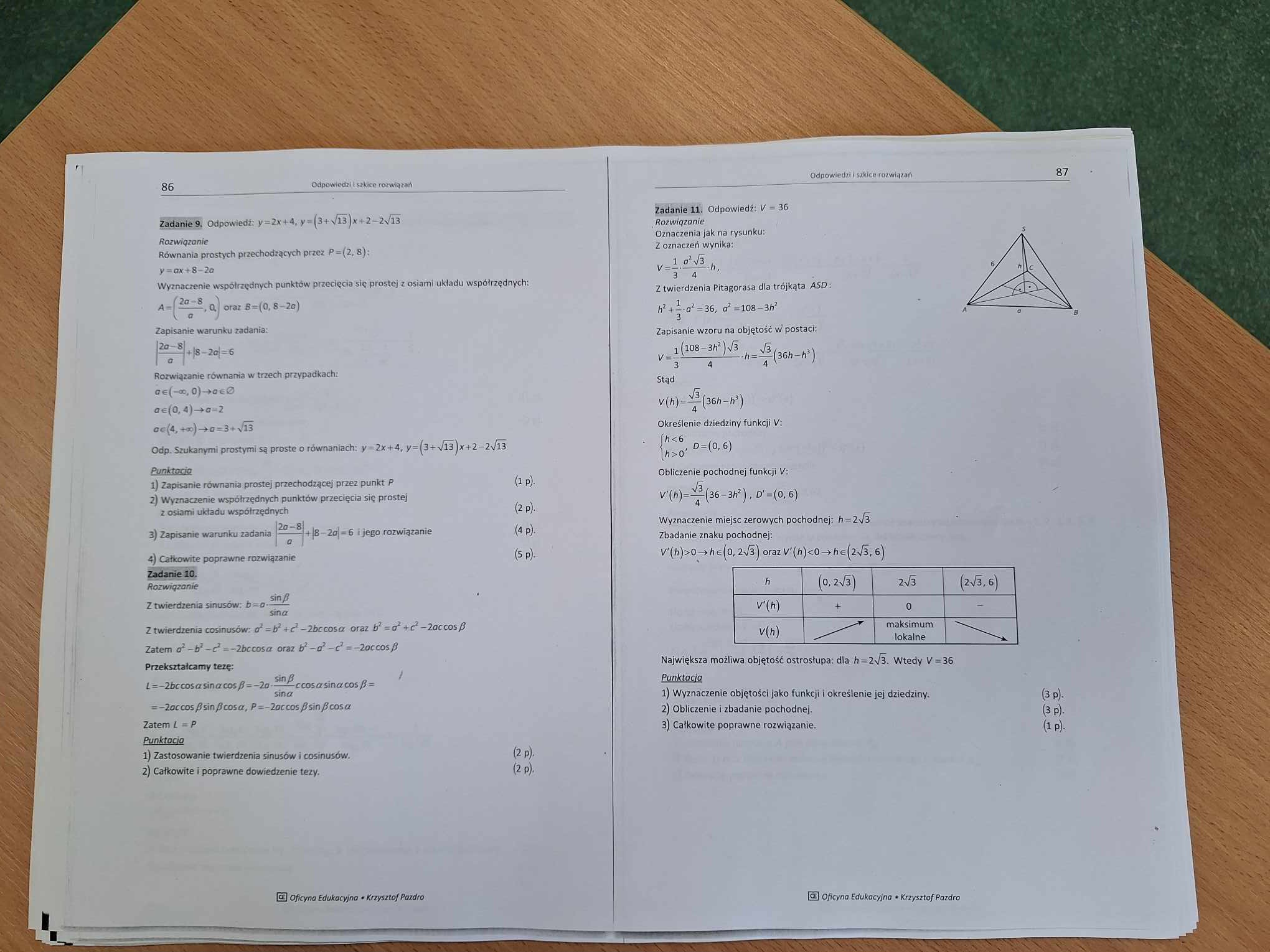 3.1:
3.1:
6:
9:
Czy te 3 zadania rozwiazalem poprawnie merytorycznie?
3.1: Nie rozumiem skąd w odpowiedziach bierze się delta=0.
6: Nie rozumiem tego tłumaczenia w odpowiedziach, ale wynik mam dobry.
9: Tutaj też niebardzo rozumiem proponowanego w odpowiedziach sposobu rozwiązania.
Matematyka pochodne Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A czy ogólnie te moje rozwiązania do zadań 3.1, 6 i 9 są poprawne merytorycznie? Bo np. w 6 doszedłem do dobrego wyniku takim trochę dziwnym rozumowaniem.
9: Nie wiem do końca skąd się biorą tam wartości bezwzględne.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur - jeżeli wyniki są poprawne to najprawdopodobniej twoje rozwiązania są okej. Traktuj forum jako miejsce w którym możesz zapytać się o coś dodatkowego/nieoczywistego. Czy jakiś fragment przede wszystkim wzbudza niepokój ? Co to znaczy "dziwnym rozumowaniem" - zadawaj precyzyjne dokładne pytania.
9 - zaznacz i prześlij dokładny fragment który jest niezrozumiały - w jaki sposób mam odpowiedzieć ci na pytanie "nie do końca wiem jakie są wartości bezwzględne" ? Czego konkretnie nie rozumiesz ?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

6: Czy tutaj można tak to rozumieć, że ekstremum nie istnieje, gdy pochodna nie ma miejsc zerowych? Szukam zatem różnych sprzeczności np dla x=1 jest asymptota a dla p+1<0 pod pierwiastkiem są wartości ujemne.

9: Skąd się biorą te wartosci bezwzględne w rozwiązaniu powyżej?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. Jeśli pochodna istnieje i nigdzie nie przyjmuje wartości 0, to nie ma tam punktów ekstremalnych, ale globalne maksimum/minimum może wystąpić wciąż na końcu przedziału albo w punkcie, gdzie pochodna nie istnieje.
2. Wartości bezwzględne pojawiają się, ponieważ w warunku zadania nie chodzi o zwykłą sumę współrzędnych punktów A i B, a o sumę ich odległości od początku układu. Musimy zatem nałożyć wartości bezwzględne.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Czy moje rozumowanie jest w takim razie prawidłowe?
Nauczony doświadczeniem z innych zadań gdzie pytają o ekstrema i nie jest to zadanie optymalizacyjne to oznacza to, że chodzi o ekstrema lokalne tak? Pytałem o to w poście Operon 2024.4.
2: Ale dlaczego nie jest to wartość bezwzględna z sumy zgodnie z wzorem na długość odcinka tylko suma wartości bezwzględnych?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. Tak
2. Jak inaczej chciałbyś to obliczyć - zaprezentuj ten warunek.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Miał Pan na myśli, że pochodna nie istnieje, ale ten x należy do dziedziny tak? Chodzi mi o wykluczenie asymptot.
2: Już rozumiem.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dla pochodnej równej zero jeśli nie ma tam ekstremum to może być asymptota lub punkt przegięcia i asymptota jest, gdy argument nie należy do dziedziny. Dlatego rozumiem, że chodzi Panu o pochodną, która nie istnieje w tym punkcie, ale ten argument należy do dziedziny (punkt przegięcia).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Musisz zadać konkretne pytanie abym mógł ci na nie odpowiedzieć. Nie wiem do czego dążysz, najlepiej na przykładzie z zadania.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chodzi o to, że jak rozumiem pochodna nie ma ektremum, gdy jest tam asymptota, argument nie należy do dziedziny (te przypadki rozpatrzyłem) lub funkcja nie zmienia znaku, bo pierwiastek jest parzystego stopnia. Z tego co widzę to w moim rozwiązaniu nie rozpatrzyłem tego ostatniego i tak się szczęśliwie złożyło, że wyszła mi poprawna odpowiedź czyli pewnie z tamtego wychodzi sprzeczność, ale jak mógłbym zapisać ten ostatni warunek?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur po raz kolejny nie wiem do końca o co pytasz, przeanalizuj to poprawne szczegółowe rozwiązanie:

- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To rozwiązanie jest taki bardzo formalne bym powiedział. A ja chciałbym dodać do swojego tylko warunek kiedy pochodna się zeruje, ale jej wykres "się odbija", bo tam miejsce zerowe jest parzystego stopnia.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie wiem o jaki warunek ci chodzi Artur.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
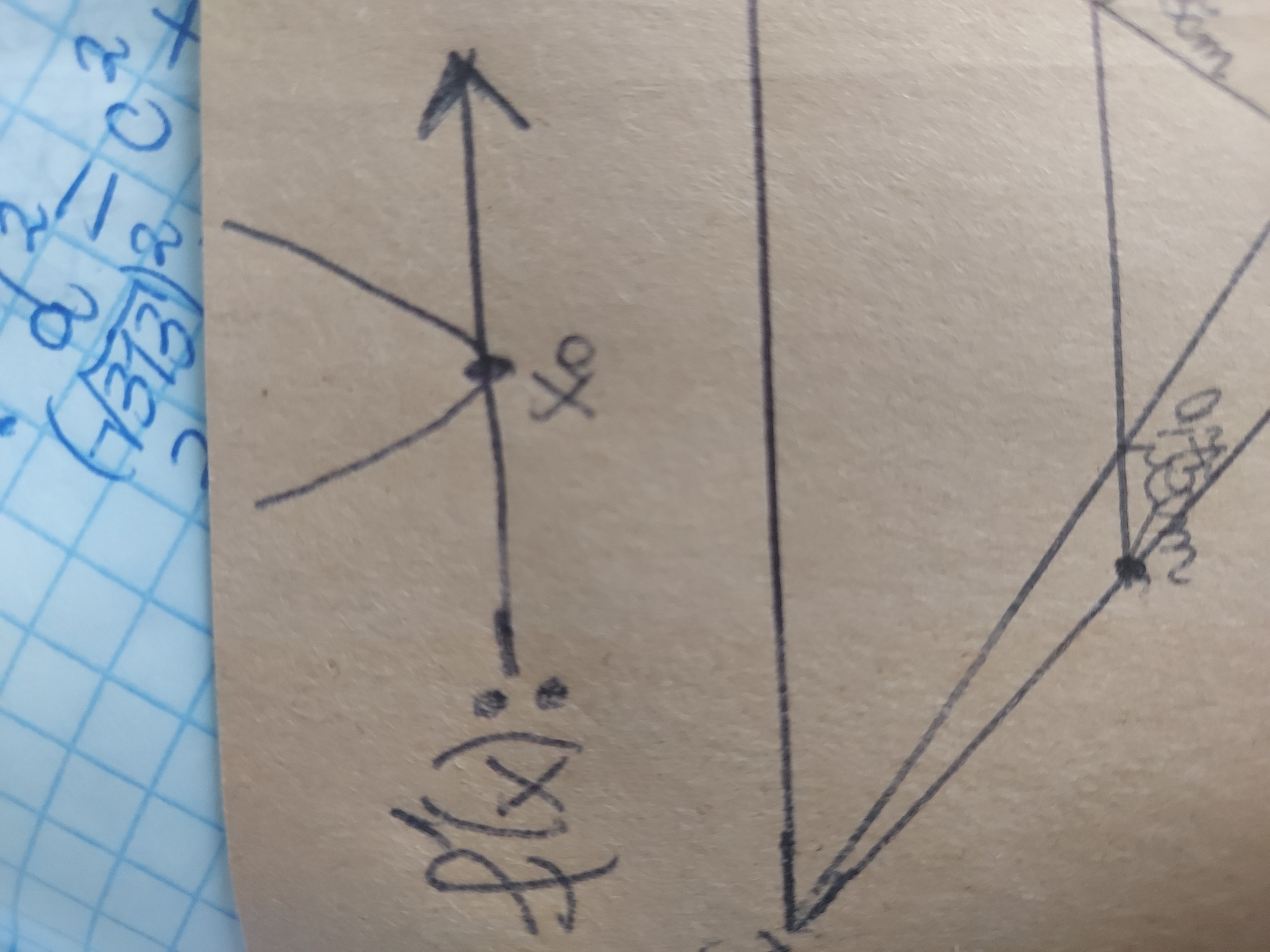
Np taki jak powyżej. Wtedy funkcja nie ma ekstremum.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To jak zapisac taki warunek? Delta_f'=0 i a_f'!=0?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale dlaczego chcesz w ten sposób to robić ? Musisz sprawdzić kiedy to wyrażenie będzie miało ile pierwiastków i czy będzie je miało. Te warunki dokladnie rozpisane są w załączniku który podałem ci wyżej.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale ja chciałbym aby moje rozwiązanie było w pełni poprawne (to które wysłałem na początku) a wydaje mi się właśnie, że tam brakuje takiego warunku tylko nie wiem jak go zapisać.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak tylko nie wiem dlaczego wchodzisz w asymptoty gdzie pytają cię po prostu o ekstrema. Wystarczy przeanalizować funkcję tak jak ci to wysłałem.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Bo w asymptocie funkcja nie ma ekstremum i to mi wyszło, że jest dla x=1, a teraz brakuje mi tylko przypadku z punktem przegięcia.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chcąc badać punkty przegięcia wchodzisz w zakres podwójnych pochodnych.
Nie ma w tym zadaniu potrzeby takiego kombinowania - zostań przy sposobie który ci pokazałem.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Okej, ale w takim razie czy mój sposób początkowy był w pełni poprawny czy właśnie zabrakło mu tego warunku?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Twój sposób jest ok, nie trzeba nic dopisywać:
Warunek na brak ekstremum lokalnego w analizie elementarnej to po prostu „pochodna nie zeruje się wewnątrz dziedziny”
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Delta = 0 bo jedno rozwiązanie.
9 - która część jest niezrozumiała ?