Arkusz2 zadania info
Wykaż, że jeżeli stosunek promienia okręgu opisanego na trójkącie prostokątnym do promienia okręgu wpisanego w ten trójkąt jest równy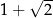 
, to trójkąt ten jest równoramienny.
Czy zamiast dowodzić że przy takim stosunku promieni trójkąt jest równoramienny prostokątny, mogę dowieść stosunek promieni w trójkącie prostokątnym równoramiennym?
trójkąt Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wykazując że stosunek w trójkącie prostokątnym równoramiennym wynosi tyle co dana w zadaniu mogę wnioskować że mając taki stosunek w trójkącie prostokątnym to jest on równoramienny. Odpowiedź w stylu twierdzenia odwrotnego to twierdzenia pitagorasa
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, możesz odwrócić tak kierunek rozumowania. Czyli obliczyć stosunek R/r w trójkącie prostokątnym równoramiennym, ale żeby spełnić treść zadania musisz pokazać, że żaden inny (nierównoramienny) trójkąt prostokątny nie daje tego samego ilorazu.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Na jakiej zasadzie miałoby to być równoważne ?