Arkusz 11 zad 2
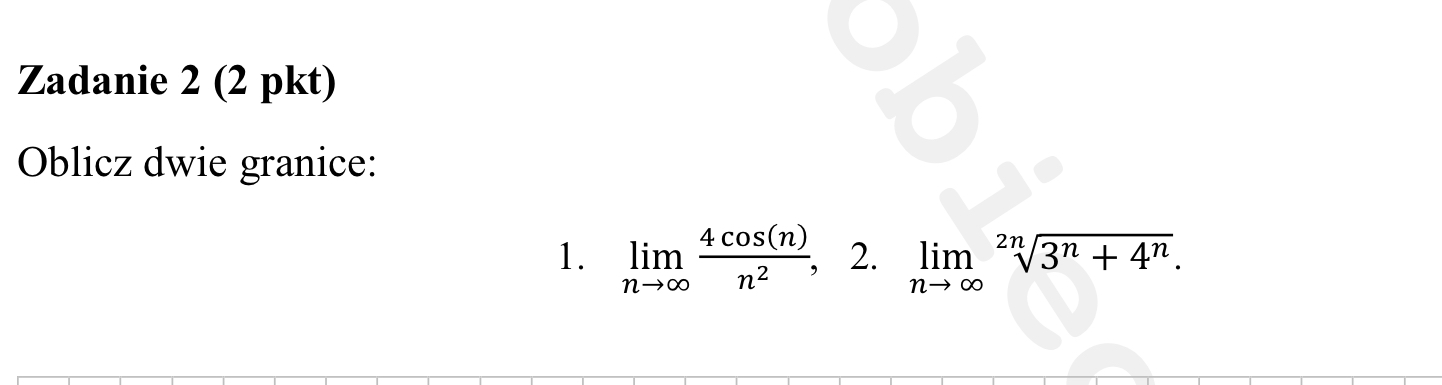
Jak to rozwiązać? Kompletnie nie ogarniam tego twierdzenia
Matura Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
czyi w 1 przykladzie za cos n wstawil pan 1 i -1?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, bo to ograniczenia dla cosinusa to -1 i 1.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W takich zadaniach korzystamy z twierdzenia o trzech ciągach, w skrócie mówi ono, że jeśli mamy 2 ciągi zbieżne do tej samej wartości to każdy ciąg który jest "pomiędzy" tymi ciągami też jest zbieżny do tego samego:
Tutaj zwykle zauważamy że sinus jak i cosinus spełniają: -1 <= cos(n) <= 1, dzięki czemu tworzymy ciąg mniejszy i większy, tak więc okazuje się, że -4/n^2 <= 4 cos(n) / n^2 <= 4/n^2, zauważmy jednak, że ograniczenie dolne jak i górne w granicy przyjmują 0, więc granica naszego ciągu tez musi być równa 0.
W drugim przykładzie ciężej jest znaleźć ciągi ograniczające, ale również się da według przedstawionego wyżej schematu, tzn: √(3^n + 4^n) >= √(4^n) i to nam daje jedno z ograniczeń, jest to dosyć oczywista nierówności. Kolejne ograniczenie będzie wynikało z sytuacji gdy "zamienimy" sobie 3^n na 4^n, czyli √(3^n + 4^n) <= √(4^n + 4^n). Kluczem jest zauważenie, że w takich przypadkach wynik zawsze zależy od największej podstawy potęgi (u nas to 4^n, bo 4^n > 3^n), stąd chcemy sprowadzić do postaci tylko z tą największą potęgą (jeśli nie do końca rozumiesz co mam na myśli to zrób kilka z pierwiastkami w podobny sposób i zauważysz, co mam na myśli z tymi wynikami).