Arkusz 6 pazdro Zad 3, 6, 10.1, 11.1






3: Jak to jest w końcu z tą monotonicznością? Czy jeśli nie ma słów "maksymalne przedziały" to zawsze w odpowiedzi muszą być nawiasy otwarte? Czy jest to kwestia dyskusyjna i nawiasy zamknięte też są uznawane?
6: Nie rozumiem dlaczego kąt ASB=120 stopni. Pewnie to w jakiś sposób wynika z kątów środkowych i wpisanych, ale czy wtedy nie powinien być on 2 razy większy od kąta ACB czyli 240 stopni? Dlaczego ES jest symetralną boku AB i dwusieczną kąta ASB jednocześnie?
10.1: Nie rozumiem dlaczego taka odpowiedź jest błędna. Przecież jeśli wykresem pochodnej jest parabola o 2 miejscach zerowych (2 razy zmienia znak) to nigdy nie będzie tak, że funkcja dla liczb rzeczywistych będzie rosła cały czas, więc nie ma takiego m moim zdaniem.
11.1: Nie rozumiem tej dziedziny w odpowiedziach i nie wiem dlaczego nie wychodzi mi taki wzór na pole, o który proszą.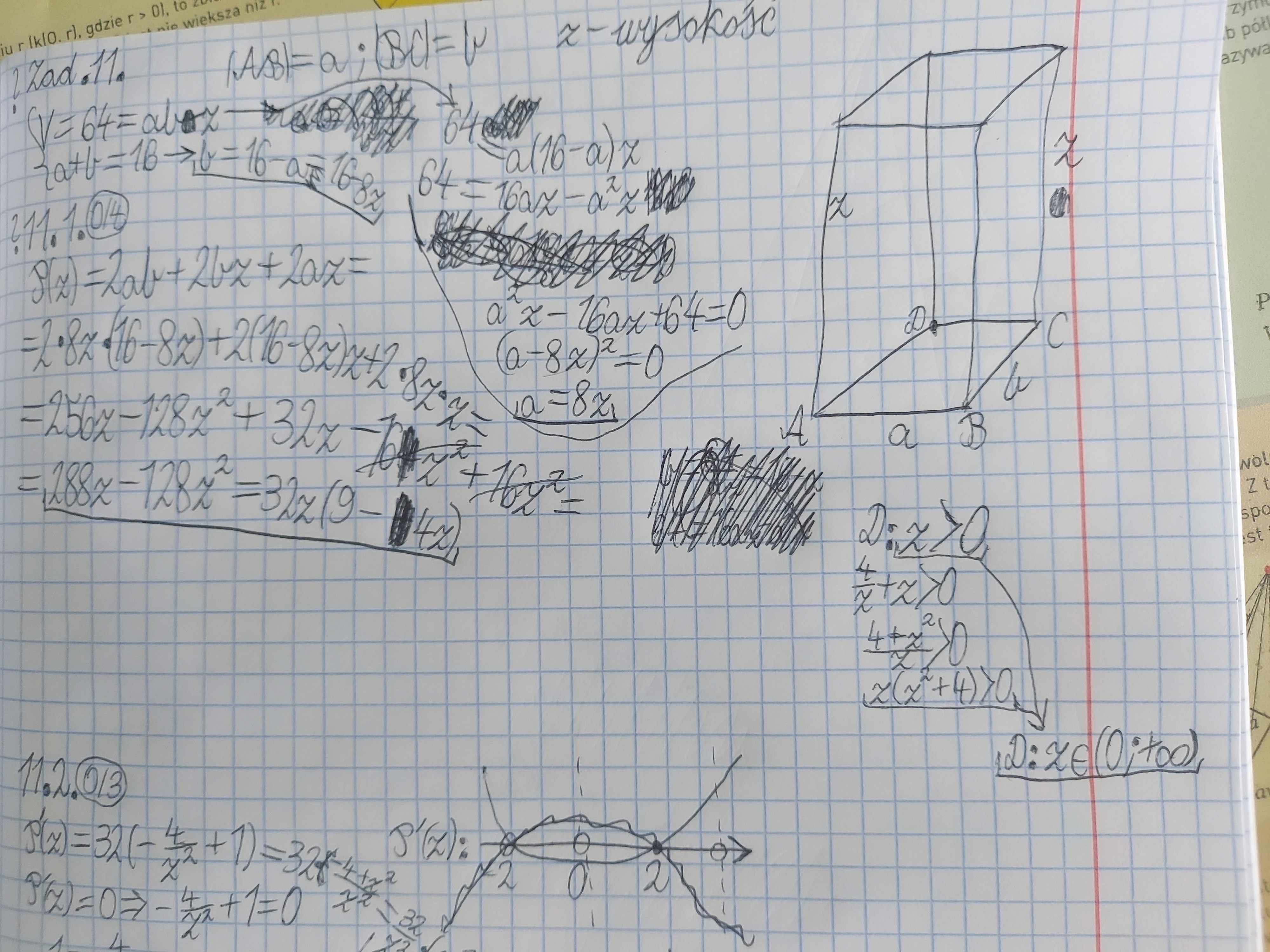
Matematyka inne Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3: Czyli rozumiem, że jakbym tak zrobił jak tutaj to byłoby ok.
6: I to, że ES jest jednocześnie dwusieczną i symetralną wynika jedynie z tego, że trójkąt ASB jest równoramienny?
Dalej nie do końca rozumiem dlaczego kąt ASB jest równy 120 a nie 240 stopni.
11.1: A z czego wynika taka dziedzina? Nie rozumiem skąd biorą się tam nierówności pomiędzy średnimi.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3. Tak.
6. Już napisałem, że masz racje co do kąta, jest błąd w odpowiedziach. Tak ES jest symetralną i dwusieczną i wynika to tylko z tego, że jest to trójkąt równoramienny.
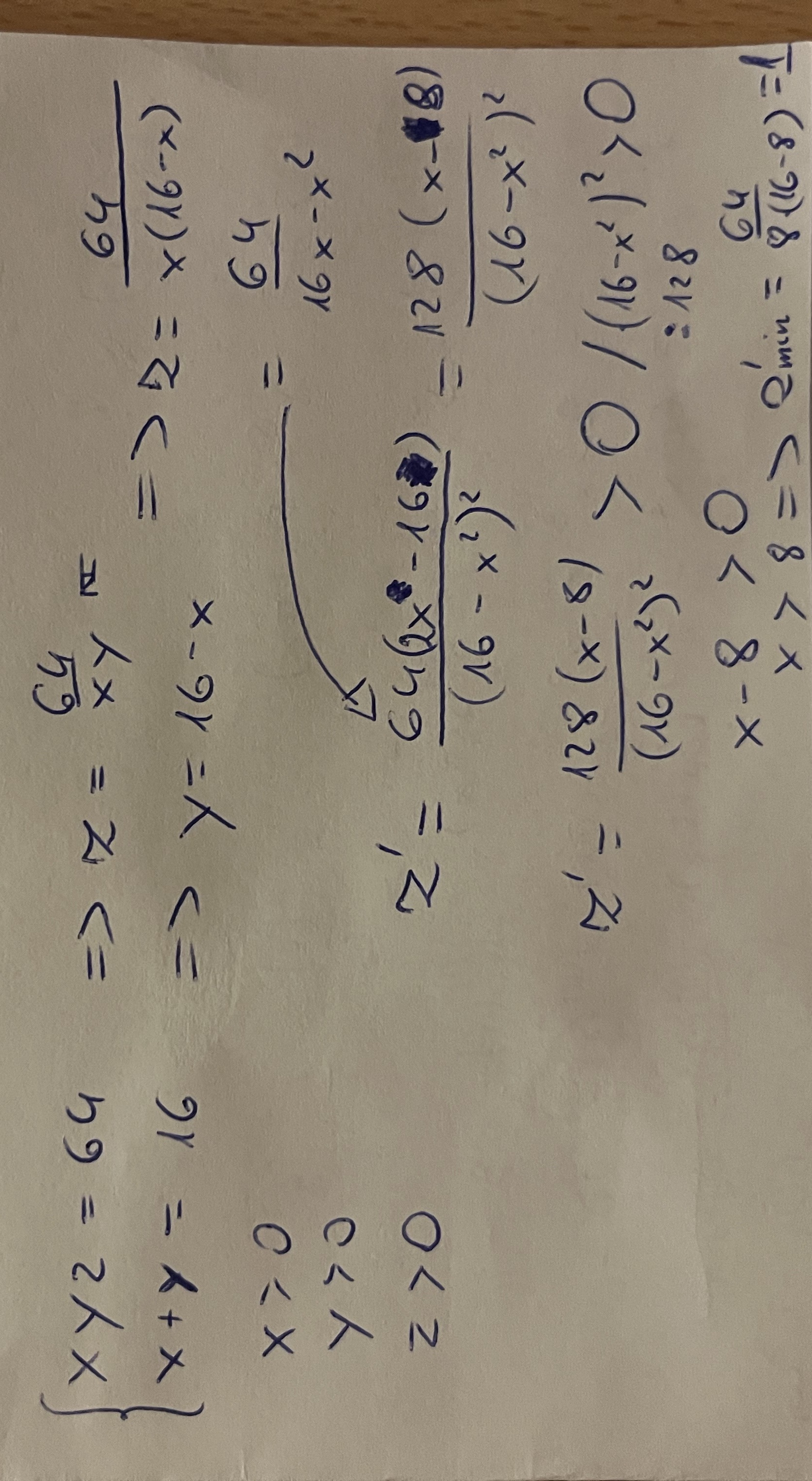
11.1. Autor zauważył, że używając nierówności między średnimi łatwiej i szybciej znaleźć ograniczenie dolne na z, można to zrobić tradycyjnie ale potrwa to dłużej. Ja wyliczyłem wpierw z od x, a następnie szukam minimum tej funkcji (uwaga na końcu zapisałem z'min = 1, powinno być zmin = 1):
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
6: No to jeśli kąt ASB jest równy 240 stopni to trójkąt ASB właściwie nie istnieje. Jak wtedy rozwiązać to zadanie?
11.1: Ale dlaczego tutaj jest optymalizacja już na etapie dziedziny?
Jak można to zauważyć, że tutaj zajdą nierówności pomiędzy średnimi?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
6. Po głębszej analizie, zadanie jednak jest dobre, tylko źle patrzyłeś na kąt:
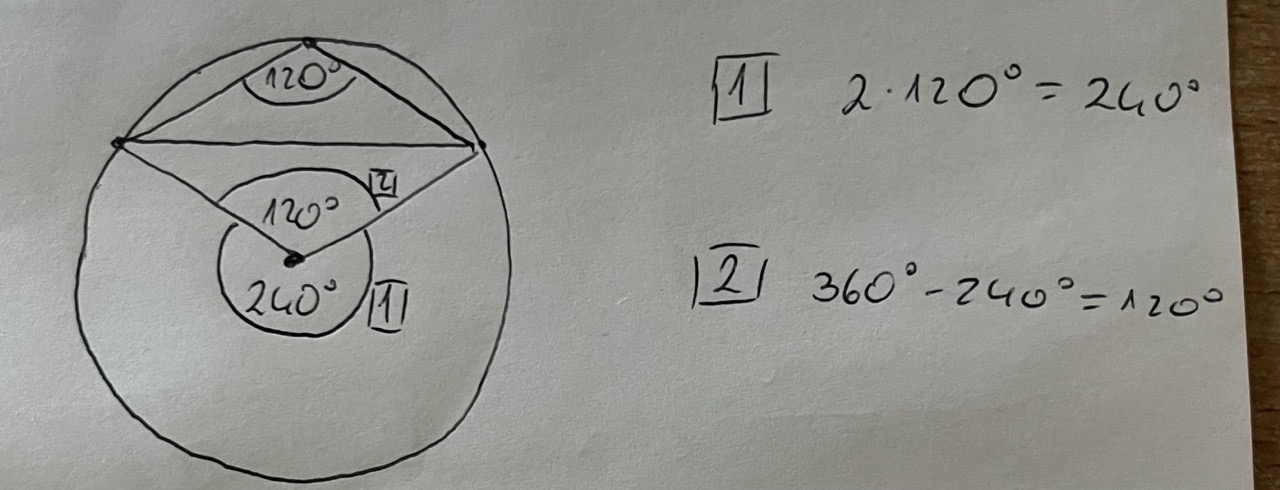
Tutaj powinieneś spojrzeć na to w taki sposób, że kąt który mnożysz razy 2 to kąt z drugiej strony czyli 240 stopni, wtedy zadanie ma sens.
11.1
Tak tutaj zaczyna się optymalizacja na poziomie dziedziny.
Nie stosuj w takich zadnich nierówności miedzy średnimi, tutaj autorowi wyszło poprawnie, ale to zbieg okoliczności, że pierwiastek z xy jest równy minimalnemu z.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
6: Czy ja dobrze widzę, że na tym rysunku wyszło, że kąt wpisany w okrąg jest 2 razy większy od kąta środkowego?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Masz racje, poprawiłem post wyżej.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Kąt środkowy odpowiadający kątowi wpisanemu w tym twierdzeniu jest zawsze z drugiej strony.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Co to znaczy z drugiej strony? Czy mógłby Pan to pokazać dla wpisanego kąta rozwartego jak wygląda wtedy środkowy na rysunku?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Masz tutaj przykład dla kąta ostrego i rozwartego:
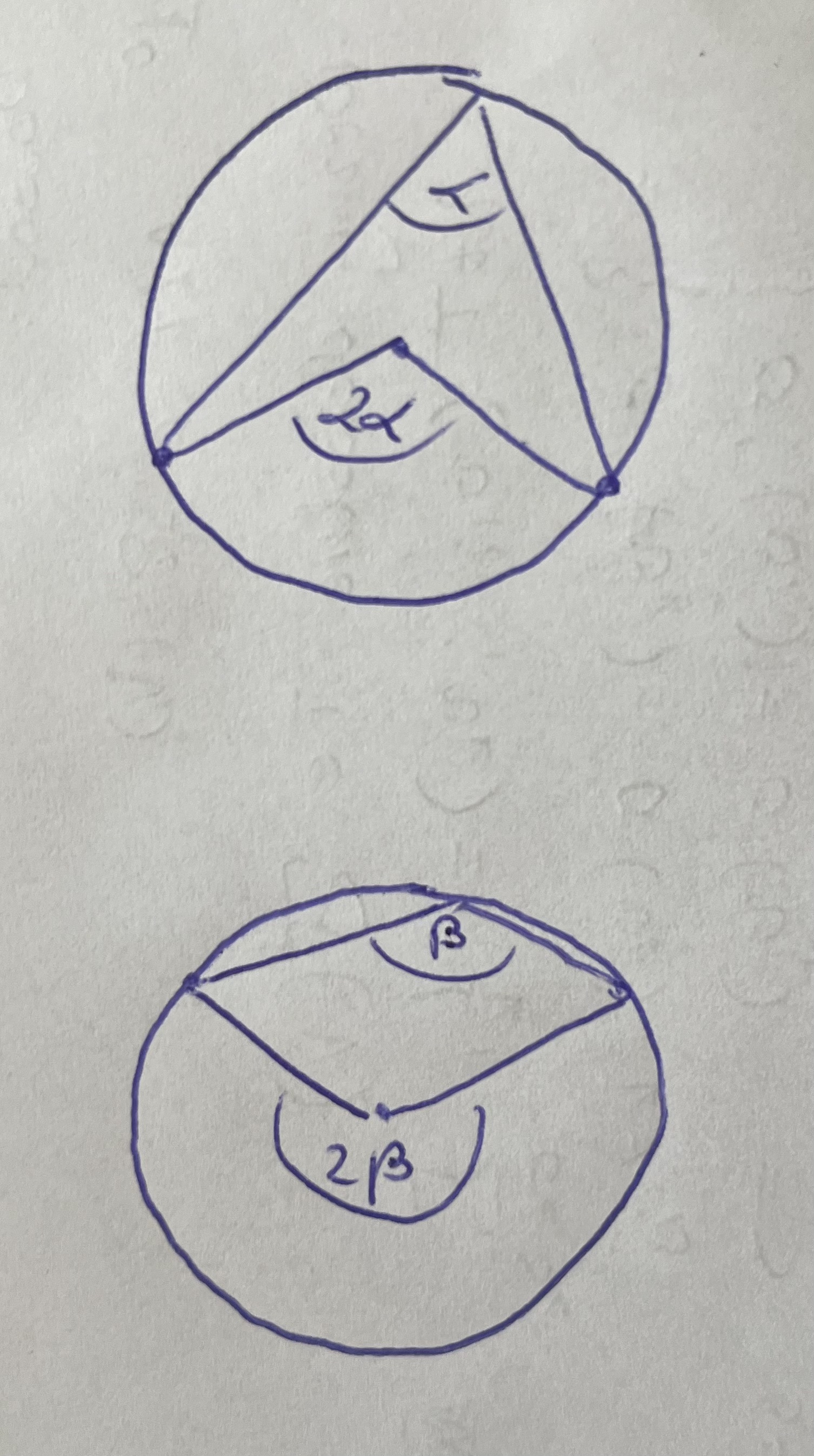
Zauważ, że oba kąty na każdy z rysunku są jakby "pod" wierzchołkiem kąta.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3: Jest to kwestia dyskusyjna, na maturze musisz wybrać sobie swoją własną metodę, czyli że albo pozostawiasz otwarte, albo pozostawiasz domknięte (z tym, że jeśli zdecydujesz się na otwarte to zawsze otwarte, a jak na domknięte to zawsze gdy dziedzina pozwala to na domknięte).
6: Masz racje co do kąta. Jest to jednocześnie symetralna i dwusieczna, bo trójkąt ASB jest równoramienny.
10.1: Zauważ, że jeśli m = -1 to oba miejsca zerowe są równe, czyli parabola nie zmienia znaku, bo ma tylko 1 miejsce zerowe.
11.1: Zauważ, że przed tym jak wyliczyłeś, że a = 8z, zastosowałeś wzór skróconego mnożenia, ale twoje z^1, a nie z^2, więc tam nie ma żadnego wzoru skróconego mnożenia.