2020.L.8

Skąd wiadomo, że E jest środkiem AD? Czy musi tak być po prostu dlatego, że trapez jest prostokątny?
Matematyka okręgi Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A jak by o to pytali to jak uzasadnić właśnie, że ten punkt E leży w środku?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zauważ, że odcinek EF jest promieniem, a E jest punktem styczności okręgu z odcinkiem AD, czyli EF prostopadłe do AB i DC, bo trapez prostokątny.
Skoro wiemy już, że EF równoległy do AB i DC, oraz wiedząc, że |CF| = |FB| (bo CF i FB to promienie) to z twierdzenia Talesa (kąt to kąt przecięcia prostych AD i BC): |DE| = |EA|.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A mógłby Pan zapisać konkretne równanie na to twierdzenie Talesa? Bo ja widzę tu tylko |CF|/|EF|=|FB|/|AB|.
Rozumiem, że oznacza Pan F jako środek okręgu. Bo u mnie S to środek okręgu. A jeśli F u Pana nie jest środkiem okręgu to nie wiem dlaczego |EF|=R.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak u mnie F to środek okręgu.
Z twierdzenia Talesa wynika też zależność o której mówiłem i którą ci tu pokażę:
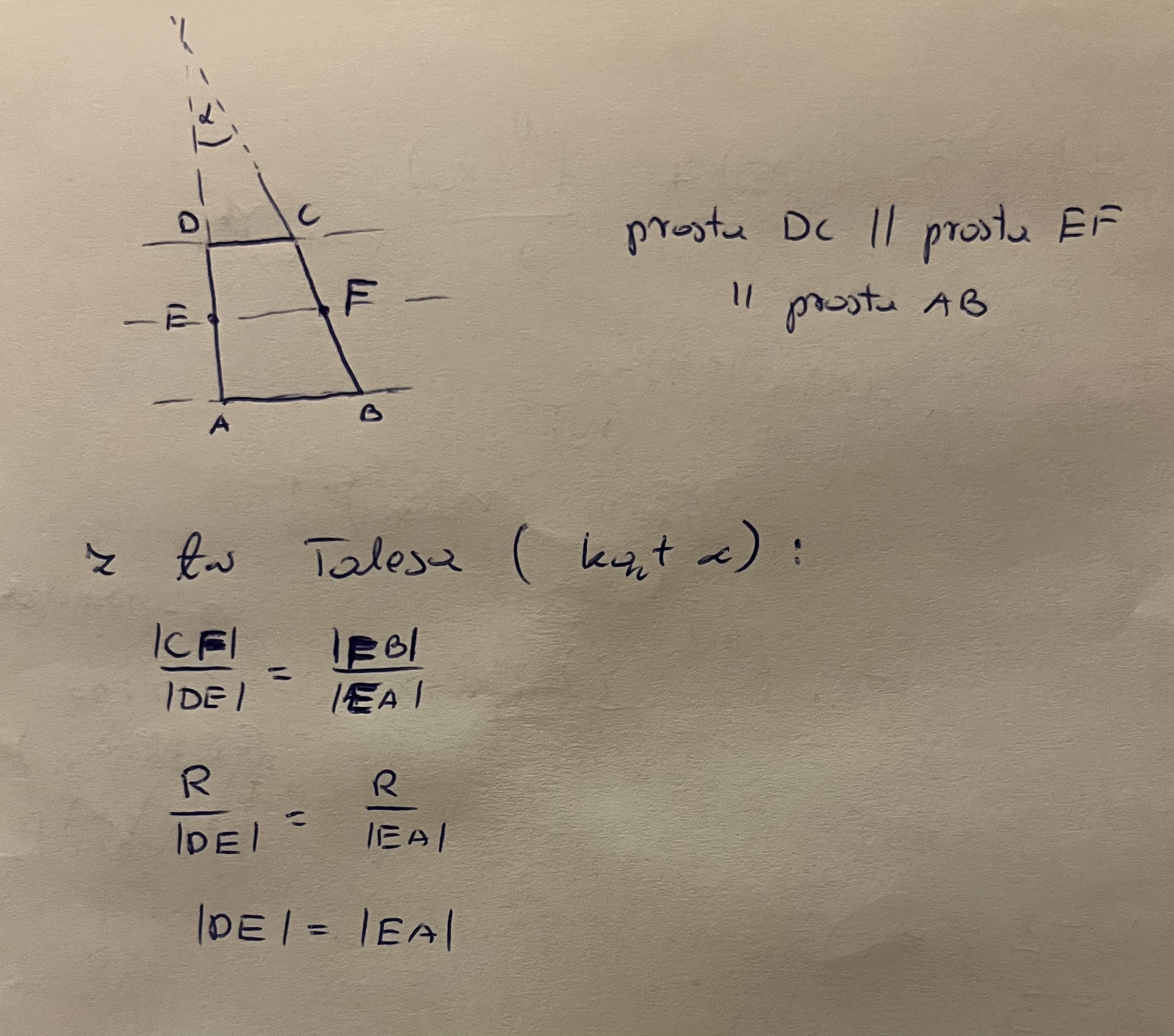
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli to jest rozumiem taka przekształcona wersja twierdzenia Talesa i ona wynika z podobieństwa trójkątów tak?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wynika z samego twierdzenia Talesa, nie potrzebujesz tam podobieństwa trójkątów.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie znam takiej metody, Euklides udowodnił korzystając z innych własności, ja u siebie mam wektorami: https://szkolamaturzystow.pl/baza-wiedzy/1609689796-twierdzenie-talesa .
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, będzie tak tutaj bo to trapez prostokątny, ale gdyby nie był prostokątny to punkt E niekoniecznie będzie środkiem.