Artur 115 wyśw. 05-05-2025 17:16

Trójkąty

Czy prawdą jest, że trójkąt jest 

  • ostrokątny, gdy a^2+b^2>c^2 i b^2+c^2>a^2 i a^2+c^2>b^2
  • rozwartokątny, gdy a^2+b^2<c^2 i b^2+c^2<a^2 i a^2+c^2<b^2?

Bo w jednym z zadań na nagraniu z geometrii analitycznej podał Pan jako jeden ze sposobów taką nierówność, tylko że dla ostrokątnego napisał Pan a^2+b^2<c^2. Czy tam jest błąd?

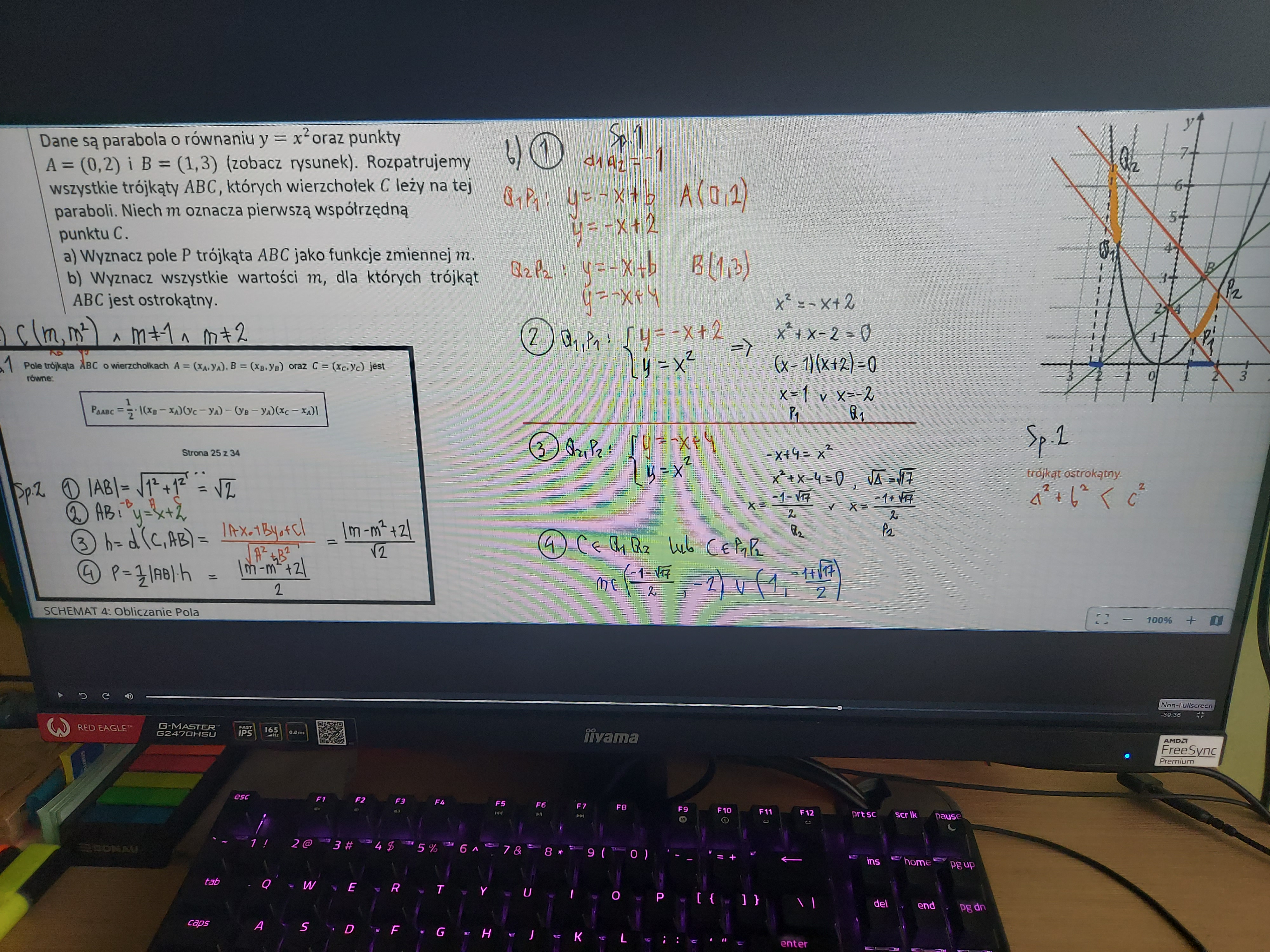
Chodzi o sposób 2.

matematyka inne Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 07-05-2025 21:50

Tak twoje kryterium dla kąta ostrego jest poprawne - dla rozwartokątnego nie do końca.

Dla rozwartokątnego wystarczy (i musi) mieć jedną nierówność „<” dotyczącą najdłuższego boku; trzy takie nierówności naraz są niemożliwe.

Artur 08-05-2025 06:04
Czyli po prostu chodzi o to, że tam jest spójnik "lub" zamiast "i"?
jarosinski 08-05-2025 12:23

Tak:

Jeżeli trójkąt jest rozwartokątny, to istnieje para boków tego trójkąta taka, że suma kwadratów ich długości jest mniejsza od kwadratu trzeciego boku.

Zadzwoń teraz Dotknij, aby się ze mną skontaktować.