Pochodna, analiza funkcji, formalności maturalne
przykładowo takie:
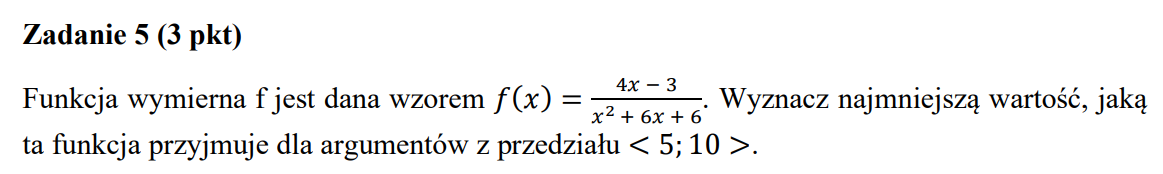
Czy przy analizie funkcji, czyli robie z tego pochodna i na dole mam funkcje zawsze >0 bo do kw. podniesiona, przy przyrownywaniu do zera musze uzasadnic czemu wezme tylko gorna funkcje do zera? Jak to oficjalnie wyglada w zapisie? Czy oznaczam ta gorna funkcje jakos inaczej np. g'(x) (czy g(x)?) i tlumacze czemu. O jakich formalnosciach ogolnie przy tego typu zadaniach trzeba dodatkowo pamietac?
Dodatkowo czy trzeba tutaj liczyć obie wartosci z kranca jezeli wiadomo po przebiegu zmiennosci funkcji ze najmniejsza wartosc przyjmnie na krancu przedzialu bo ciagle maleje?
rozniczkowy Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
czyli licze wtedy granice lim x->koniec granicy (f(x))?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie wiem co masz na myśli przez "koniec granicy f(x)".
Jeśli masz dziedzinę (a; b) i podejrzenie, że dla x = b, może być mniejsza wartość niż twoje znalezione minimum lokalne to liczysz granicę przy x-> b z lewej strony. Jeśli natomiast masz podejrzenie, że w x = a to zachodzi to liczysz granicę przy x -> a z prawej strony.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Co do mianownika wystarczy byś zaznaczył, że >0 (możesz to zrobić klamerką lub strzałką, nie musisz pisać tego słownie), potem masz dowolność.
Co do liczenia wartości krańcowych to liczysz je tylko wtedy kiedy mogą coś zepsuć, jeśli widzisz, że funkcja maleje przez cały czas to nie musisz liczyć wyższego krańca, bo wiesz, że nie będzie on niższy od drugiego. Ważne też, że gdy mamy otwarte nawiasy w dziedzinie to licząc krańcowe wartości stosujemy granice jednostronną.