Ola 25 wyśw. 11-05-2025 20:50

2017.N.13


Jak wyglądałoby rozwiązanie tego zadania korzystając z prawdopodobieństwa, nie kombinatoryki? Próbowałam, ale prawdopodobieństwo wychodzi>1 i nie wiem czemu

Matematyka matura poziom rozszerzony Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 11-05-2025 21:15

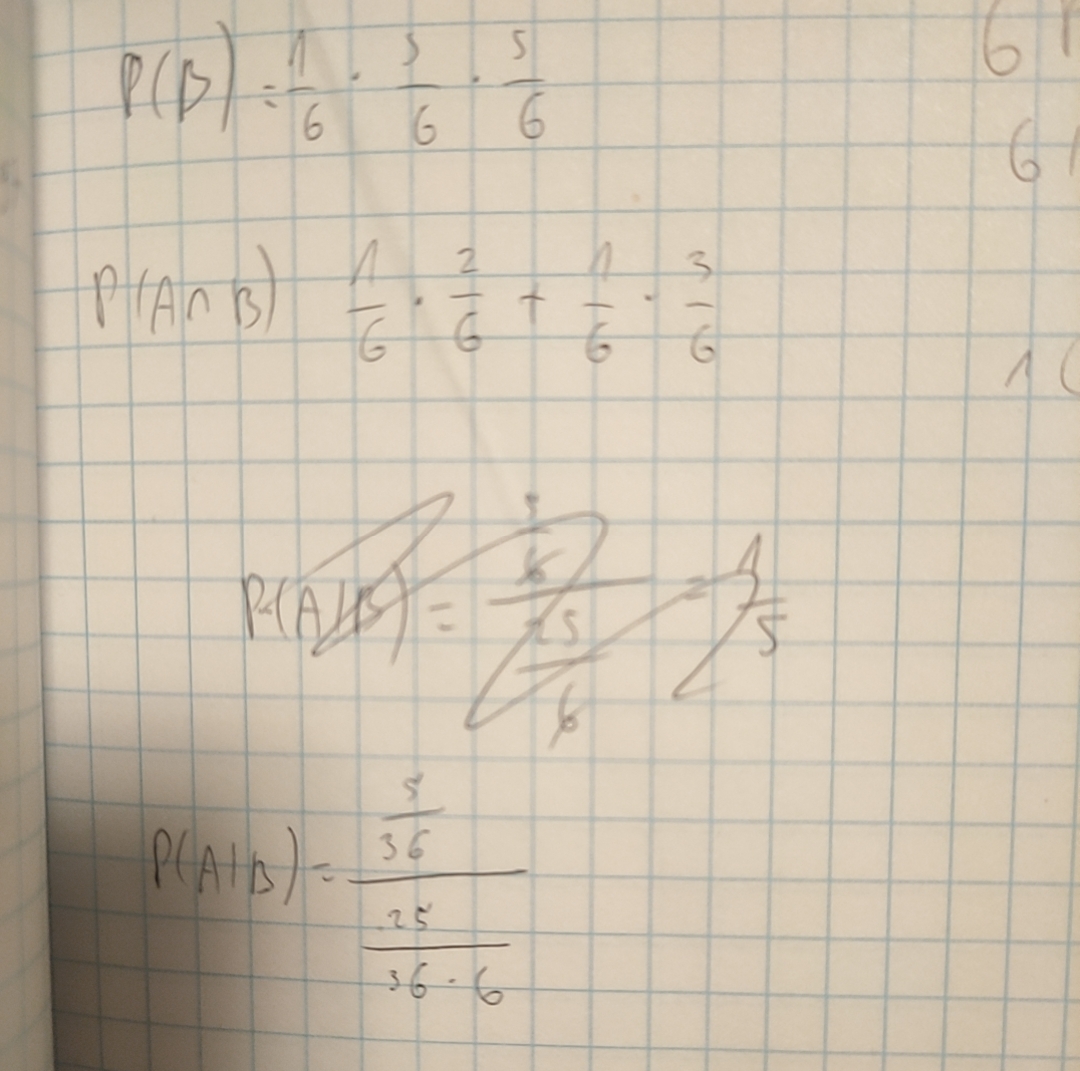
Takie zadania na maturze raczej powinno się rozwiązywać z prawdopodobieństwa klasycznego (tzn kombinatorycznie), bo punkty są przyznawane za np policzenie |Omega|.

Natomiast jeśli cię interesuje podejście jak to nazwałaś prawdopodobieńswem to zauważ, że :

P(B) = 1/6 * 5/6 * 5/6 * 3!, należy przemnożyć przez 3!, bo ważna jest kolejność (6 może wypaść na pierwszej, na drugiej, na ostaniej kostce itd)

Natomiast P(A iloczyn B) = 1/6 * 2/6 * 2/6 * 3! + 1/6 * 3/6 * 3/6 * 3!,

bo łączymy 2 sytuacje, czyli:

1. Gdy mamy 1 szóstkę i 2 parzyste inne niż 6 liczby na pozostałych, czyli 1/6 jako 6, 2/6 jako inne niż 6,

2. Gdy mamy 1 szóstkę i 2 nieparzyste i analogicznie.

Ola 11-05-2025 21:42

Dziękuję!