Wfais_UJ 2022

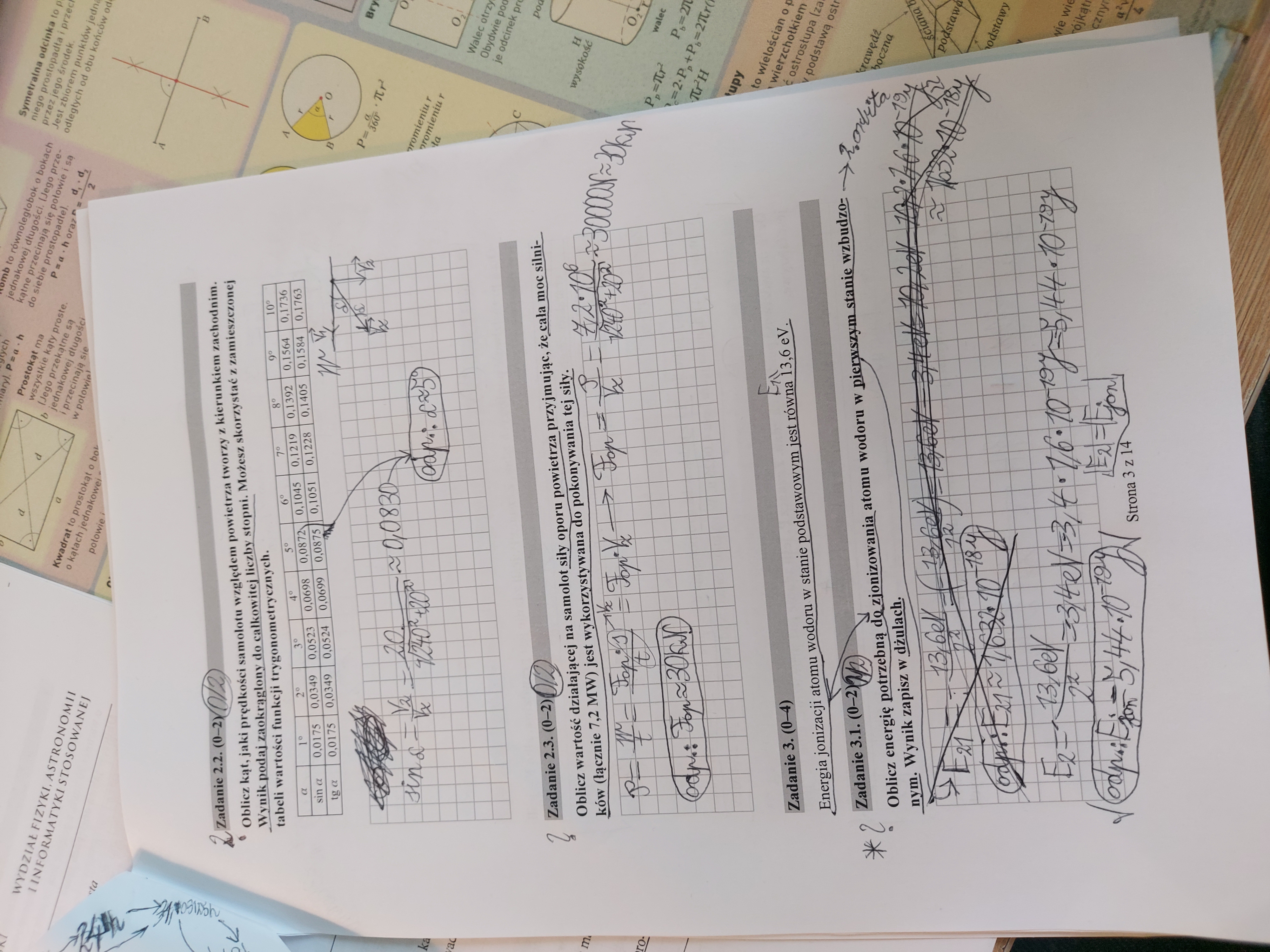


1: Kompletnie nie rozumiem tego zadania. Poza tym, że w każdą dobę statek przepływa 480km wydaje mi się, że nie da się tego zadania rozwiązać maturalnymi możliwościami, tutaj wyjdzie zapewne jakiś ciąg, bo przecież z każdym dniem droga do przebycia przez gołębia się zmniejsza.
2: Dlaczego moja interpretacja tych wektorów jest błędna?
3.1: Czy pisanie E2 i Ejon jest ze sobą tożsame? Bo właściwie widzę, E znaki są tylko przeciwne. Czy zatem możemy pisać E2 i Ejon bez wartości bezwzględnych?
4.2: Czy w tym zadaniu konieczne jest uwzględnienie ciepła?
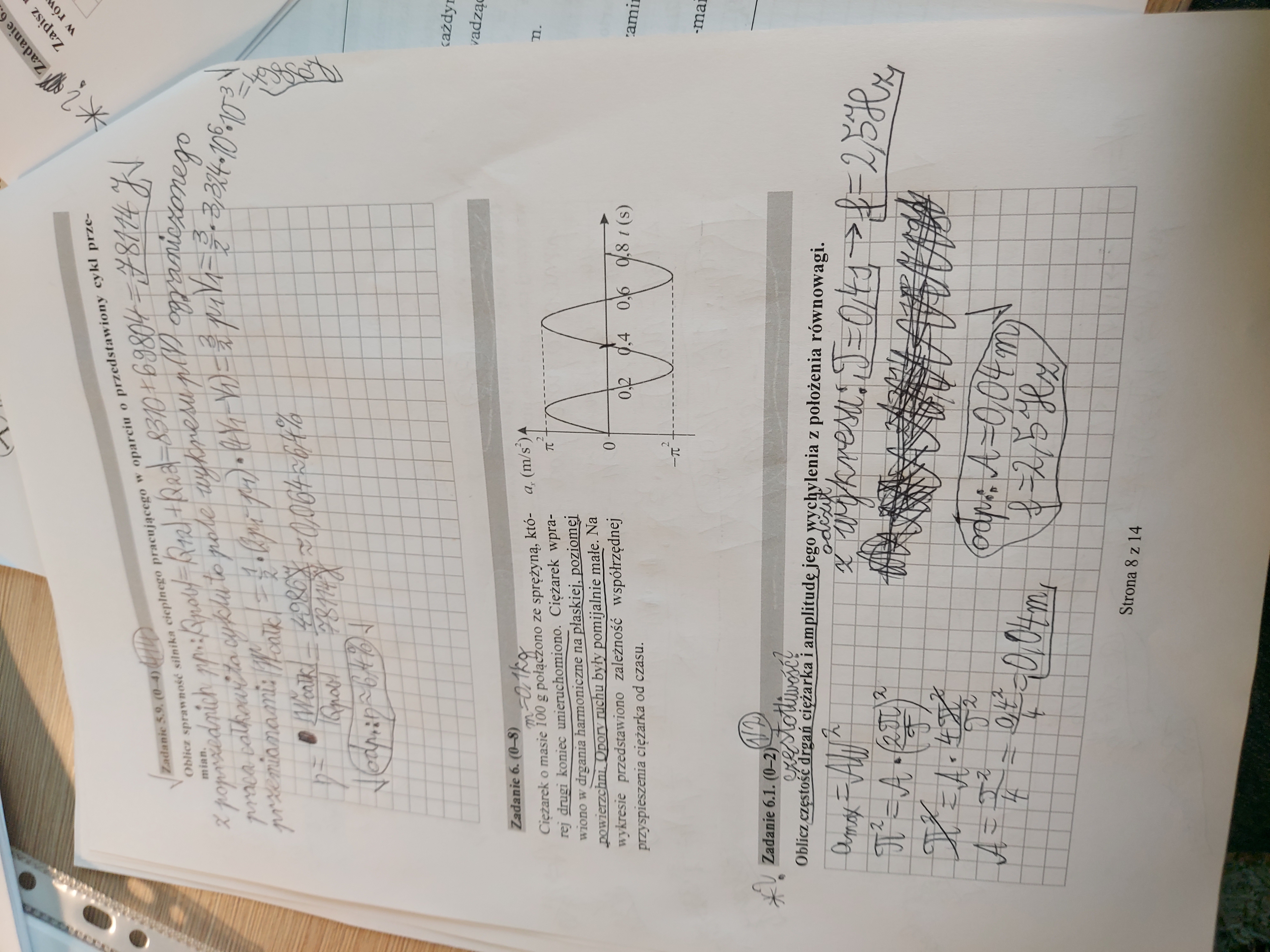
6.1: Czy częstość drgań to prędkość kołowa? Bo ja spotkałem się z powiedzeniem częstość kołowa, ale samo słowo częstość myślałem, że oznacza częstotliwość. Czy na maturze będzie to bardziej doprecyzowane?
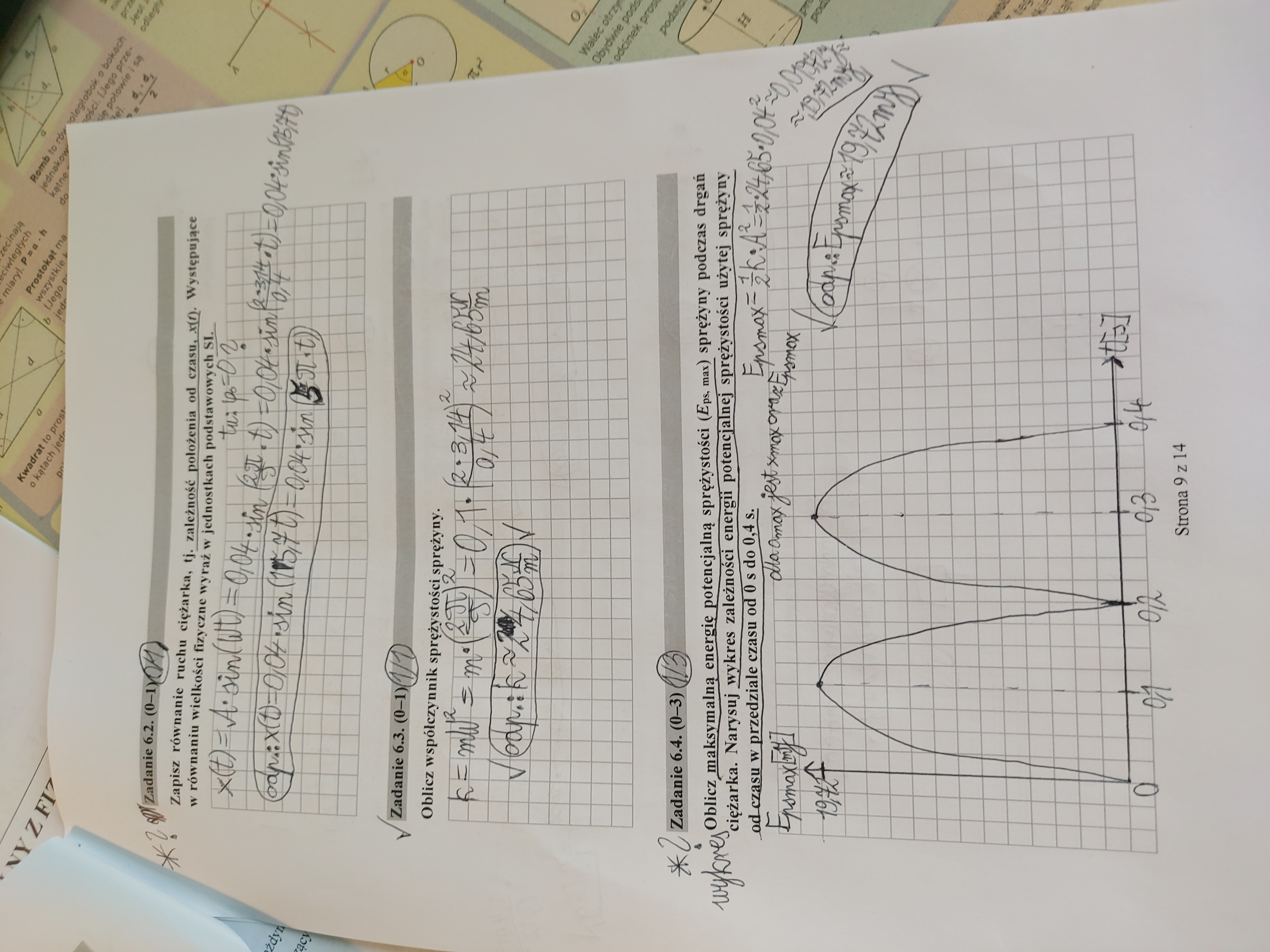
6.2: Czemu faza początkowa w tym zadaniu jest równa pi? Przecież wykres sinusoidy a(t) zaczyna się od punktu (0;0).
6.4: Czy taki wykres byłby uznany? Czy musi być gładszy? Bo rozumiem, że jest to funkcja y = |sin x|.
6.5: Dlaczego pierwsze zdanie jest fałszywe?
7: Czy w tym zadaniu niepewności względne muszą być sobie równe? Bo ja tak założyłem i mi wyszło, ale nie wiem dlaczego tak jest.
8: Czym jest potencjometr? Czy jest to opornik suwakowy? Czy mogą nas o takie rzeczy pytać na maturze?
Fizyka inne Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Trochę nie rozumiem. Wtedy gołąb będzie obserwatorem? Trzeba zapisać wzory na zbliżanie się gołębia i statku oraz statku "goniącego uciekającego od niego gołębia"?
2: Faktycznie z tym V2 mi się pomyliło, ale V1 przecież zgodnie z treścią powinno być dokładnie w kierunku zachodnim.
4.2: W odpowiedziach je uwzględnili. Czyli rozumiem, że jak będzie to wymagane to o to poproszą.
6.1: Czyli tylko na prędkość kołową są inne nazwy, a na częstotliwość nie ma?
6.2: Rozumiem, że to czy da się fi0=+pi czy -pi to nie ma znaczenia, bo funkcja powtarza się co 2pi. Ale czy tak samo byłoby gdyby funkcją trygonometryczną zamiast sinusa był cosinus?
6.4: A dlaczego (sin x)^2?
7: Czyli nie trzeba na maturę wiedzieć jak działa prawo przenoszenia niepewności?
8: Czyli taki układ byłby poprawny?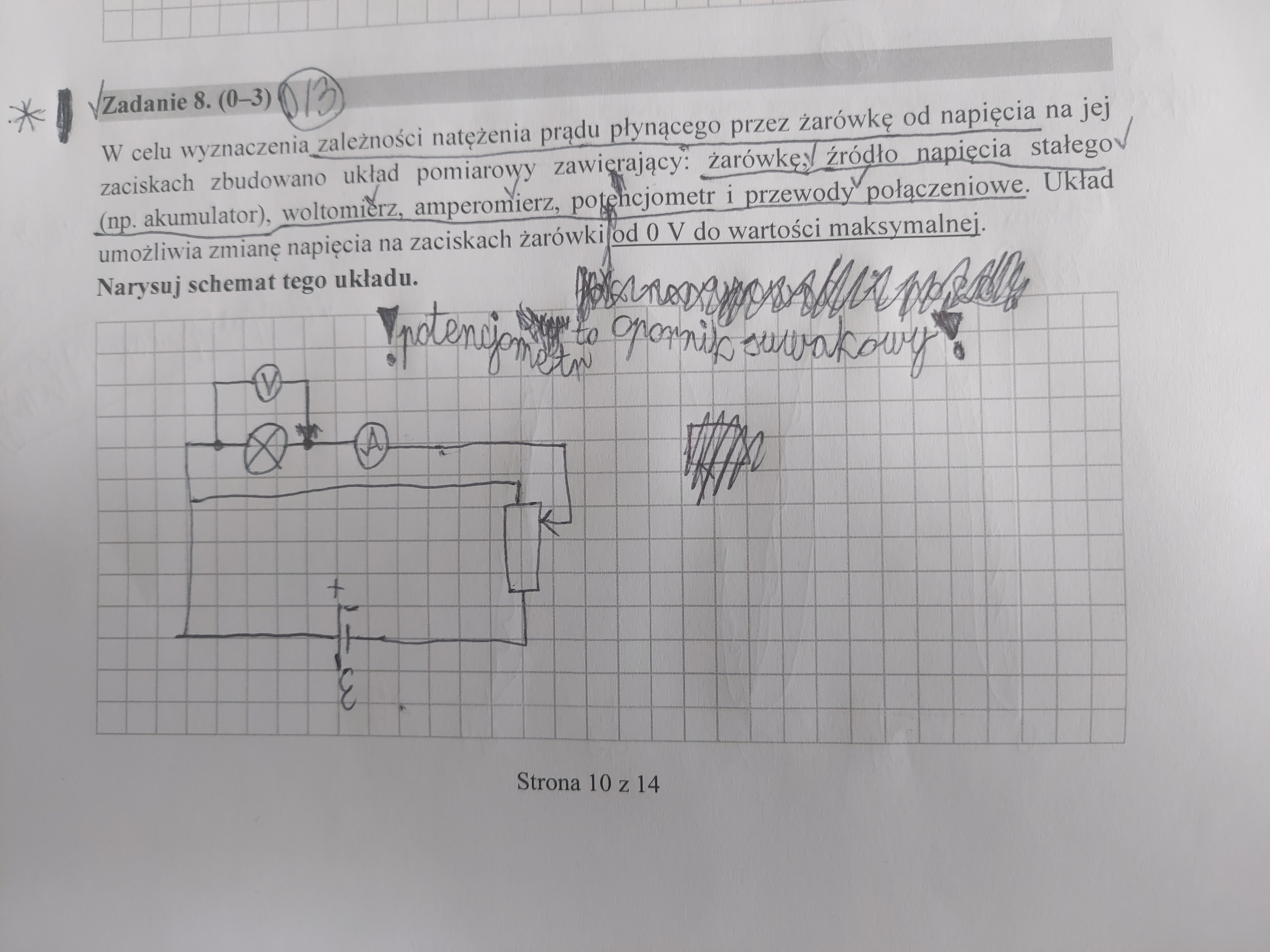
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Nie, tak jak napisałem gołąb jest falą. Obserwatorem jest rodzina na brzegu rejestrująca falę, czyli gołębie. Statek jest źródłem. I zapisujesz wzory na efekt Dopplera dokładnie tak jak one widnieją w karcie, nie trzeba nawet nic modyfikować.
2: W kierunku zachodnim samolot porusza się względem Ziemi, a v1 to predkość samolotu względem powietrza.
4.2: Tak, poproszą (choć nigdy to się nie pojawiło do tej pory).
6.1: Częstość kołowa to nie zawsze prędkość kołowa, choć czasem to to samo. W każdym razie zawsze wyrażamy je wzorem 2*pi/T, czy też 2*pi*f. Nie ma innej nazwy na częstotliwość (przynajmniej żadnej popularnej).
6.2: Tak, nie ma to różnicy, w którą stronę. W przypadku cosinusa to już oczywiście będzie miało znaczenie (wynika to z faktu jak wygląda funkcja cosinus).
6.4: Bo Eps = 1/2 * k * x^2, a przecież x = A*sin(wt)
7: Nie trzeba.
8: Tak, jest ok.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Faktycznie to działa, ale dość trudno na to wpaść. A jak rozumować tutaj "kinematycznie"? Nie rozumiem proponowanej odpowiedzi.
2: Ale przecież jest napisane: "Samolot lecący dokładnie w kierunku zachodnim porusza się względem powietrza z prędkością V1..." Dla mnie taka informacja wskazuje na fakt, że wektor V1 jest dokładnie na zachód.
6.1: Ale w kontekście maturalnym to zawsze to samo?
6.2: To tutaj, w którą stronę jest przesunięty ten wykres o pi?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Aa bo ja nawet nie patrzyłem wcześniej na rozwiązanie podane przez autorów i od razu przyszedł mi do głowy efekt Dopplera. A da się to faktycznie zrobić "kinematycznie". No więc tak jak oni to liczą, to można sobie obliczyć jaką drogę pomiędzy wysłaniem kolejnych gołębi przebywa statek (delta_s). Oznaczmy sobie prędkość gołębia jako v. A to oznacza, że wysyłając np. drugiego gołębia nie znajduje się on w odległości równej v*24 h od pierwszego gołębia, ale w nieco mniejszej. O ile mniejszej? A no o tyle, ile przebył w tym czasie statek (czyli właśnie delta_s). Stąd różnica odległości między kolejnymi gołębiami jest o tyle mniejsza, że przekłada się to na zmniejszenie ich odstępu czasowego do 18 h.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
2: No cóż, może jest to trochę niefortunnie zapisane, ale jak dla mnie jednak powiedzenie, że samolot leci w kierunku zachodnim oznacza, że jest to kierunek zachodni względem ziemi, a nie powietrza ;)
6.1: Zawsze to samo w sensie takim, że zawsze zapisujemy to w tymi wzorami, które wymieniłem. Ale przecież np. mając prąd zmienny mamy tam częstość kołową omega, a nie jest to przecież żadna prędkość kątowa żadnego ciała.
6.2: no nie da się tego jednoznacznie stwierdzić - albo w lewo albo w prawo, bo efekt jest ten sam ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: To próbowałem liczyć to w podobny sposób, ale wyszło mi, że ten odstęp czasu będzie różny za każdym razem. Co miałem źle w tamtym rozwiązaniu (pierwsze zdjęcie tego posta)?
2.1: I to zawsze trzeba wiedzieć czy będzie trochę bardziej doprecyzowane, bo ja zazwyczaj mam tego typu problem z określeniem tych wektorów w ruchu względnym?
2.3: Dlaczego tutaj ma być V1 w mianowniku a nie Vz?
6.2: Ale chodzi mi o funkcję cosinus. Czyli np jak mielibyśmy zapisać równanie V(t) to jakby ono wyglądało?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Szczerze mówiąc nie jest w stanie "ogarnąć" Twoich obliczeń - bardzo to wszystko jest chaotycznie zapisane i nie za bardzo wiem jaki tu jest tok rozumowania i kolejność obliczeń (ani co jest czym). Gdybyś mógł to zapisać w bardziej "przystępny" sposób, to byłoby mi zdecydowanie łatwiej się do tego odnieść.
2.1: Nie wiem czy na maturze bardziej by to doprecyzowali szczerze mówiąc... być może, ale gwarancji nie daję ;)
2.3: Bo skoro rozpatrujemy siłę oporu powietrza i związaną z nią pracę, to interesuje nas prędkość samolotu względem powietrza właśnie.
6.2: No to cosinusa też trzeba by przesunąć o +pi albo -pi. Więc to by było: v(t) = A*w*cos(wt +/- pi)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Może część na tym zdjęciu jest przejrzysta. Początkowo statek ma drogę "s" do przebycia. 1 dnia przepłynie ss1d=Vs*t=480km. Liczę czasy lotu gołębi w czasie kolejnych dni (rozumiem, że gołąb po przylocie do portu wraca na statek): 2. dzień: t_g2=(2*(s-ss1d))/Vg ; 3. dzień: t_g3=(2*(s-2ss1d))/Vg ; a zatem n-ty dzień: t_gn=(2*(s-(n-1)*ss1d))/Vg i powstaje tego typu ciąg z niewiadomymi t_gn, s oraz n.
6.2: No ale stwierdziliśmy wcześniej, że przy cosinusie miałoby to znaczenie czy + czy -.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Ale gołąb nie wraca przecież na statek, skąd to założenie? Gołąb dolatuje do portu i tyle. I mamy policzyć co jaki czas kolejne gołębie dolatują do portu.
6.2: Sorry, to był mój błąd, przy cosinusie to też nie ma przecież znaczenia (oczywiście jeśli ciągle mówimy o przesunięciu o pi - przy innych wartościach przesunięcia to już oczywiście może mieć znaczenie).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: A dlaczego miałbym założyć, że gołąb nie wraca? Nie ma w treści napisane ani, że wraca ani, że nie wraca.
6.2: Nie no chyba ma to znaczenie, bo pi to nie jest cały okres tylko połowa.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: No ale skoro nie ma nic napisane, to po co wprowadzać sobie dodatkowe założenie, które jeszcze utrudnia obliczenia? To w takim wypadku równie dobrze można założyć cokolwiek innego ;)
6.2: Właśnie dlatego, że to jest połowa to nie ma to znaczenia. Zresztą widać to łatwo z wykresu - weź sobie wykres cosinusa i przesuń go najpierw w prawo o pi, a potem w lewo i zobaczysz, że dostaniesz w obu przypadkach to samo.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: To prawda, że droga, którą muszą przebyć gołębie ciągle się zmniejsza, ale my nie musimy wcale liczyć czasu lotu każdego kolejnego gołębia :) mała podpowiedź: można tu zastosować wzory na efekt Dopplera. Statek to źródło fali, a gołębie to kolejne grzbiety emitowanej fali - mamy zatem prędkość źródła, prędkość fali i częstotliwość fali (okres to 24 h) - i na tej podstawie możemy to zrobić :)
2: Zgodnie z treścią wiatr wieje z kierunku południowego, czyli wektor v2 musi być zwrócony w górę (zakładając, że na dole jest południe). Samolot porusza się dokładnie na zachód (zakładamy, że względem ziemi), więc wektor v3 musi być w lewo. No a teraz skłądamy prędkości (jak z łódką na rzece): prędkość samolotu względem ziemi = prędkość samolotu względem powietrza + prędkość powietrza względem ziemi. To jest oczywiście równanie wektorowe, więc wektorowo mamy: v3 = v1 + v2. Stąd tak muszą ukłądać się te wektory jak to jest w odpowiedziach.
3.1: No pewnie by to przeszło, natomiast formalnie w istocie E2 ma znak ujemny, a Ejon dodatni.
4.2: Niee, CKE tego nigdy nie chce.
6.1: Nie będzie to bardziej doprecyzowane, to już jest precyzyjna nazwa i trzeba to pamiętać - częstość kołowa, czy ogólnie częstość to zawsze jest omega. Częstotliwość to f.
6.2: Ale zgodnie ze wzorem na przyspieszenie mamy a(t) = -A*w^2 * sin (wt + fi0). Czyli gdyby faza początkowa była zerowa, to wykres powinien zachowywać się jak minus sinus, czyli staruje faktycznie od (0,0), ale musiałby zaczynać od pójścia w dół. A tu wygląda to jak sinus (z plusem), a to oznacza, że jest to -sinus przesunięty o pi, stąd taka faza początkowa.
6.4: To nie jest wartość bezwzględna z x, ale sin(x) podniesiony do kwadratu. Więc formalnie nie powinno być tam takich ostrych zakończeń, ale może by to przeszło, to nie matematyka ;)
6.5: Na początku ruchu ax staje się dodatnie, czyli przyspieszenie tuż po rozpoczęciu ruchu ma zwrot zgodny z osią x (powiedzmy, że to jest w prawo). Ciało startuje z położenia równowagi (bo początkowe przyspieszenie jest zerowe). Ponieważ a jest w prawo, to wychylenie musi być w lewo (wychylenie ma zawsze w ruchu harmonicznym zwrot przeciwny do przyspieszenia), czyli ciało ruszyło w lewo, więc w stronę przeciwną do zwrotu osi x.
7: Tak właśnie akurat wychodzi, choć formalnie wynika to z prawa przenoszenia niepewności - raczej ogólnie nie spodziewałbym się takiego zadania na maturze.
8: W pewnym uproszczeniu tak, potencjometr to jest opornik suwakowy. Nie trzeba tego wiedzieć, z pewnością napiszą to w poleceniu czym to jest (a jeśli już to pewnie i tak użyją po prostu sformułowania opornik suwakowy). A opornik suwakowy już jak najbardziej pojawić się może, choć raczej nie spodziewałbym się, że trzeba będzie narysować układ z takim opornikiem - on tam po prostu w jakimś układzie może być już umieszczony i wtedy wystarczy pamiętać, że gdy "skracamy" ten opornik przesuwając suwak, to zmniejszamy jego opór i analogicznie gdy go "wydłużamy", to zwiększamy jego opór.