Artur 122 wyśw.
25-06-2025 13:41
6.190
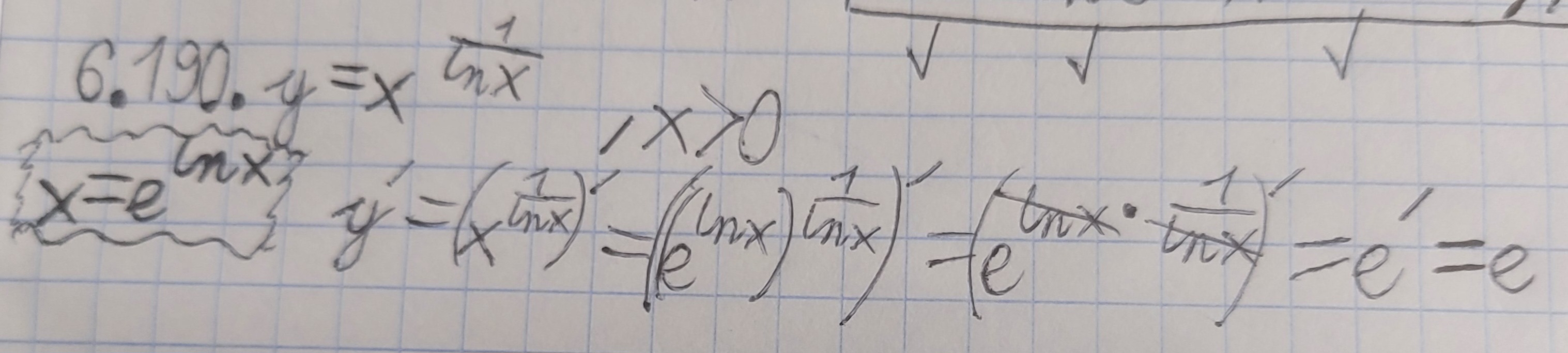
Mamy wzór (e^x)'=e^x. Możemy podstawić x=1. Dlaczego zatem w odpowiedziach jest e'=0 a nie e'=e?
Poza tym co to znaczy "wyjaśnić wynik"?
Matematyka pochodna funkcji złożonej Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski
25-06-2025 23:09
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur
26-06-2025 20:17
No ale mówiliśmy, że "e" jest specjalną liczbą, która podniesiona do dowolnej potęgi (np. 1) i zróżniczkowana da tą samą liczbę (e^x)'=e^x.
Czy w takim razie np. (e²)'=0, bo e² to też jest stała? Jeśli tak to moim zdaniem wtedy wzór (e^x)'=e^x jest bez sensu.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jarosinski
30-06-2025 10:42
Artur
01-07-2025 13:20
Zgodnie z wzorem (e^x)'=e^x moim zdaniem powinno być jednak (e^1)'=e^1=e.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jarosinski
07-07-2025 23:27
nie, pochodna ze stałej wynosi 0
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur
08-07-2025 09:08
Okej, a (e²)' też jest równa 0?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jarosinski
08-07-2025 21:19
Tak, ponieważ jest to stała - liczba
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur
09-07-2025 13:28
e jest stałą. Pochodna ze stałej to 0