2025C.1.3

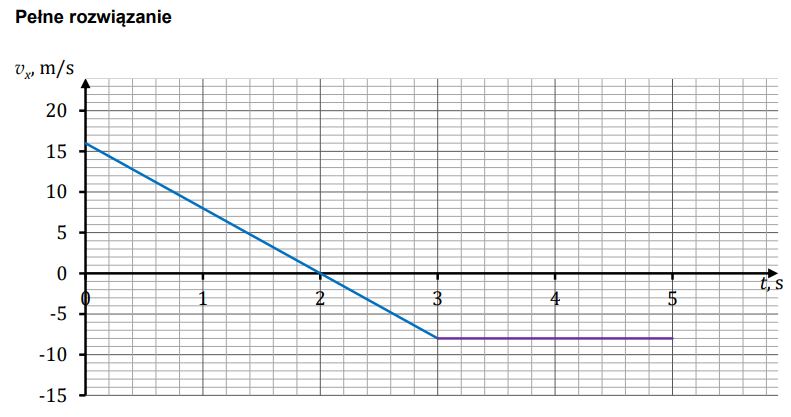
W tej sytuacji w istocie obliczone wartości (punkty na wykresie) należy połączyć linią, bo wiemy dokładnie z jakim rodzajem ruchu mamy w danym etapie do czynienia, co wynika z podanych w treści równań. Natomiast ten podpunkt tego zadanka mamy przewidziany do zrobienia dopiero po naszych drugich zajęciach, na których to właśnie powiemy sobie jak w takich sytuacjach należy sobie radzić. Ale żeby nie było, że niczego tu nie podpowiem, to w tej sytuacji trzeba spojrzeć na równania x(t) podane w treści zadania. W pierwszym przypadku (x(t) = 4 + 16t - 4t^2) można zinterpretowac przecież jako x(t) = x0 + v0*t - at^2/2, a zatem oznacza to, że jest to ruch jednostajnie opóźniony (stąd wykres v(t) będzie funkcją liniową, ale malejącą). Drugi etap to z kolei x(t) = 40 - 8t, co nalezy zinterpretować jako x(t) = x0 - v*t, więc jest to ruch jednostajny, a zatem prędkość będzie w nim stała. W efekcie wykres ostatecznie powinien wyglądać jak na załączonym obrazku:

dziękuję