2025C.1.2
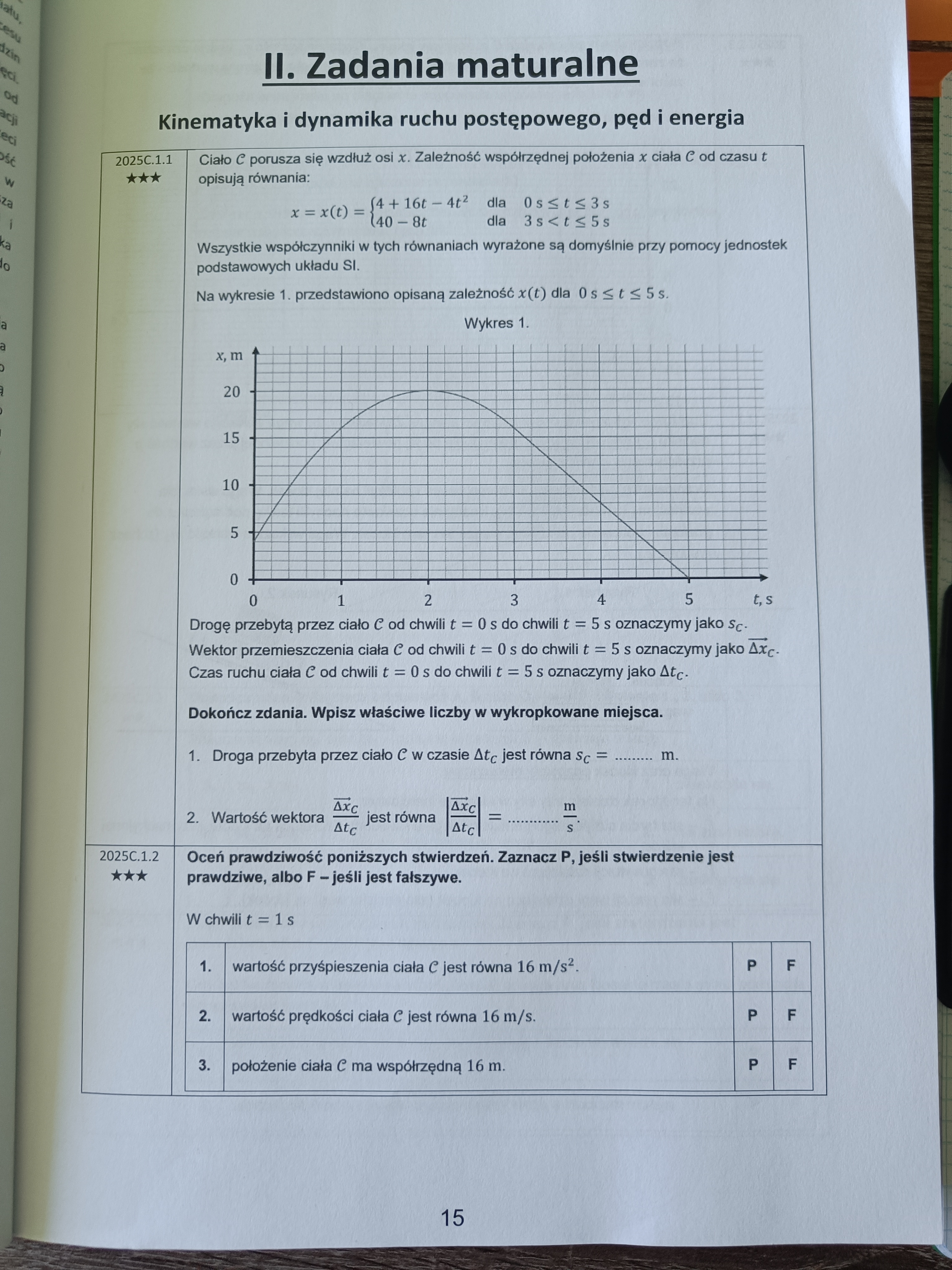
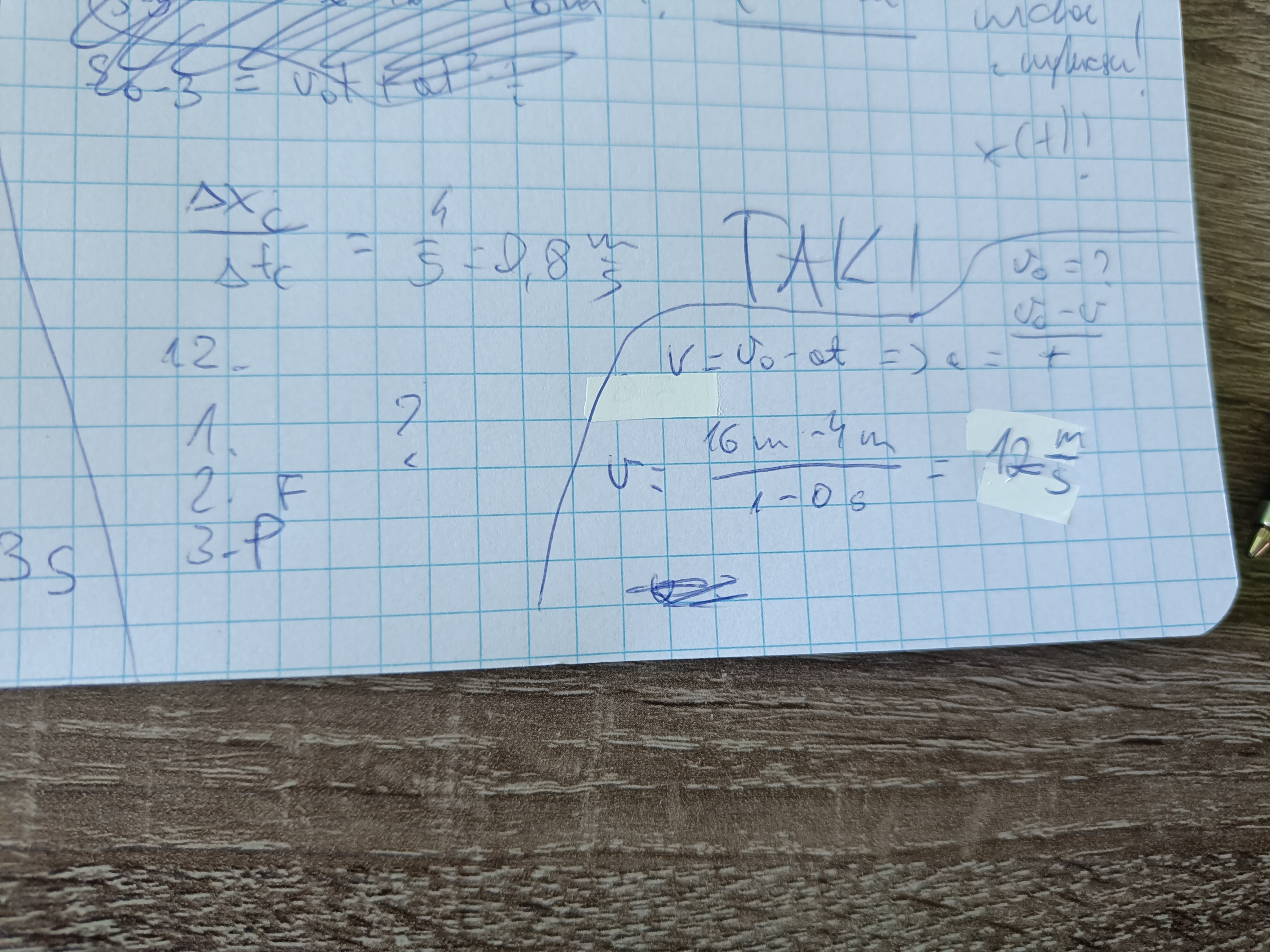
Próbuję zrobić zadanie 1.2 i nie jestem pewien odpowiedzi. Jestem pewien, że 3 punkt to prawda, bo widać to na wykresie w chwili t=1s, odnośnie drugiego punktu nie jestem pewien czy mogę to liczyć to z definicji, ale jeśli tak to wychodzi mi fałsz, natomiast jak mogę wyliczyć pierwszy punkt? Jak wyliczyć przyśpieszenie? Mogę jakoś skorzystać z funkcji kwadratowej podanej wyżej?
czy takie rozwiązanie tego zadania jest prawidłowe? Dużo bardziej ogarniam matmę, więc sposób z pochodną jakoś bardziej mi leży
kinematyka zadanie maturalne Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Oczywiście możesz stosować tutaj fakt, że prędkość to jest pochodna położenia po czasie, jest to jak najbardziej poprawne merytorycznie rozwiązanie :) i z niego faktycznie widać, że drugie zdanie jest fałszywe i pierwsze również (bo w istocie przyspieszenie jest równe -8 m/s^2 gdy mówimy o jego współrzędnej x-owej, a to oznacza, że jego wartość to po prostu 8 m/s^2). Gdybyś natomiast nie chciał używać pochodnych (bo oczywiście nie ma takiego obowiązku), to należałoby się zorientować, że skoro x(t) jest kwadratową funkcją czasu, to jest to ruch jednostajnie zmienny. Wiemy to chociażby z tego jak wygląda równanie na drogę w ruchu jednostajnie zmiennym (s = v0*t +/- at^2/2). Z niego wynika również, że to co stoi przy t to jest v0, a to co stoi przy t^2 to jest a/2. Możemy zatem stąd odczytać v0 i a, no a ponieważ wiemy już, że jest to ruch jednostajnie zmienny (dokładnie: opóźniony), to prędkość po czasie t możemy zapisać jako v(t) = v0 - a*t. Wstawiamy tu odczytane wcześniej v0 i a oraz t = 1 s i mamy także prędkość.