Wojciech 83 wyśw. 15-10-2025 19:50

Zadanie domowe 5 cz. II zad 1

Wyznacz wszystkie wartości parametru m dla których równanie 

(X+3)[(2m+1)x^2-2(m-2)x+m-2]=0

ma trzy różne rozwiązania rzeczywiste x1, x2, x3 spełniające warunek x1x2x3 > 0 

W jednym z warunków x1x2 > 0

wyszło mi m€(-♾️;-1/2)u(2;+♾️). A w odpowiedziach jest od (-1/2;2). 

Robił ktoś już to i wyszło mu tak lub inaczej?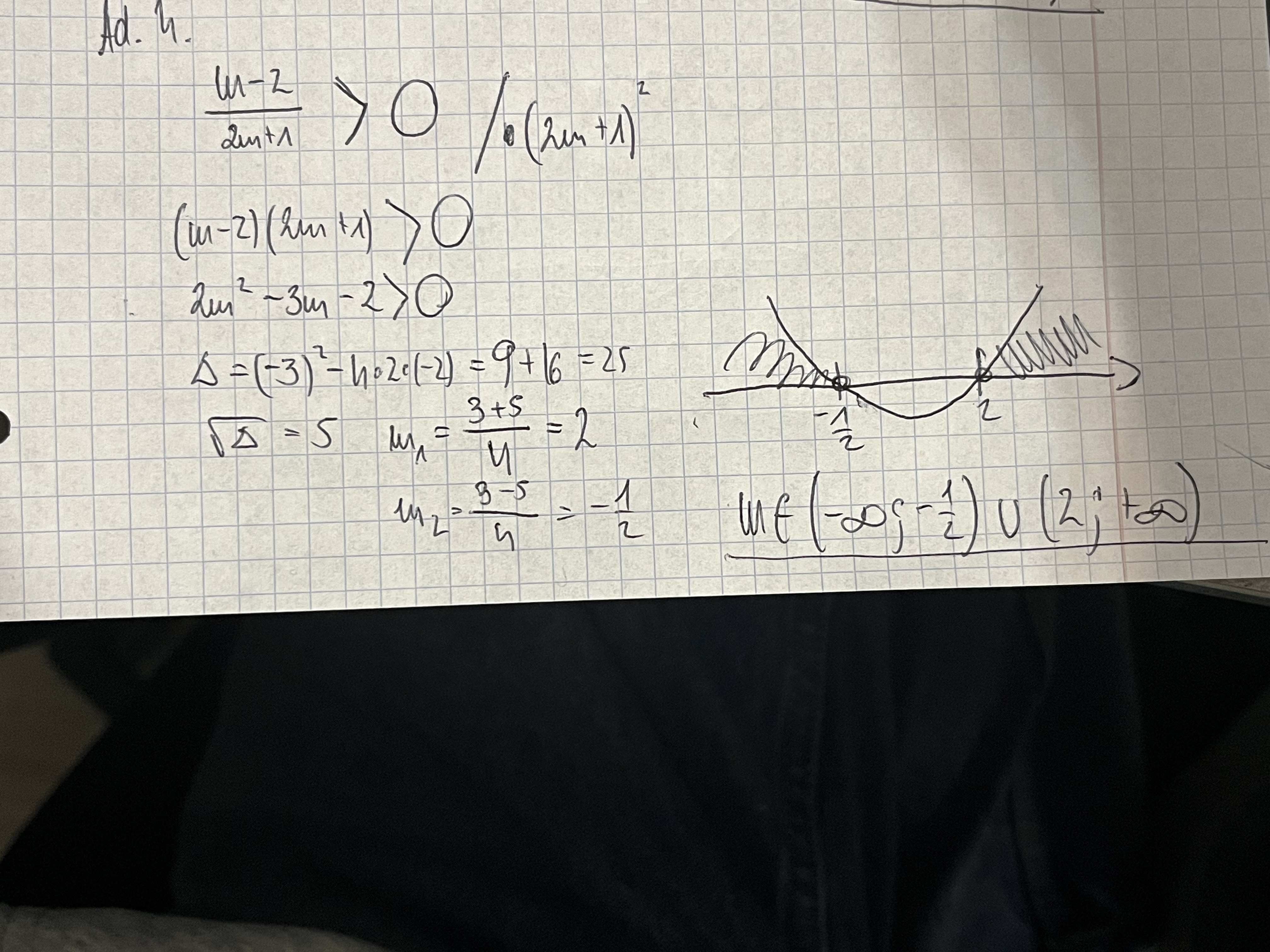 

Matematyka rozszerzona domowe Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Zuzia 15-10-2025 22:08

Hejka, ja  ten warunek to zapisałam jako x1*x2<0, i widziałam, że w kluczu jest x1*x2>0 ale nie rozumiem dlaczego, bo jedno miejsce zerowe to x=-3, a jak mamy spełnić warunek x1*x2*x3 >0 to mając już jedną liczbę ujemną to te dwie pozostałe powinny być jedna dodatnia druga ujemna, bo iloczyn dwóch liczb ujemnych daje dodatnią liczbę, razy liczba dodatnia jest to na pewno >0. i jak zapisze sie taki warunek na x1*x2<0 to rozwiązaniem jest faktycznie (-1/2 ; 2) czyli tak jak w kluczu. Zastanawiam się czy w książce zdarzyła się pomyłka z tym zwrotem, czy ja nie coś źle rozumiem.