Zadanie domowe nr 5 zadanie 6 c
W odpowiedziach mamy
I tutaj mnie zastanawia
Udowadniamy że f(x2) - f(x1) <0 zgodnie z tym że x1<x2
Rozpatrując to że nasz x1,x2 należy do przedziału x1,x2∈(-∞;+3) sprawdźmy do czego możemy dojść
Skoro w naszym liczniku wychodzi nam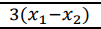 
gdzie wiemy że nie ważne jaką liczbe podstawimy ze zbioru ona zawsze będzie ona dodatnia x1 zawsze będzie musiał być większy od x2 więc ich różnica musi być dodatnia
A nasz mianownik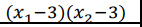 
musi być liczbą dodatnią 
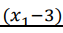nie ważne co podstawimy za x1 z naszego przedziału x1,x2∈(-∞;+3) on musi wyjść ujemny tak samo z 
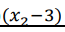Skoro oba nawiasy wyjdą ujemne cały mianownik musi być dodatni
Zgodnie z moją dedukcją skoro licznik i mianownik jest dodatni
To całe wyrażenie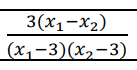 
>0 co nie zgadza się z naszym dowodem.
Może ktoś mi pomóc zrozumieć co poszło w mojej dedukcji nie tak, mógłby ktoś podać kontr przykład?
matematyka rozszerzona wielomiany praca domowa Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Już rozumiem o co chodzi nie zwróciłem uwagi na to że że skoro ma to być funkcja malejąca to dla coraz większych x jej wartość f(x) jest coraz mniejsza dlatego moje rozważania do niczego nie prowadziły. Rozpatrywałem to tak jakby to była funkcja rosnąca mój błąd.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale x₁ < x₂, więc wyrażenie w liczniku 3(x₁-x₂) <0, zatem licznik jest ujemny, przy czym mianownik jest faktycznie dodatni, dlatego cały ułamek jest ujemny.