Zadanie domowe nr 6, zadanie 4, podpunkt 3b
4. Tarczę szlifierską w postaci obrotowego krążka o promieniu 8 cm i masie 650 g wprawiono w ruch obrotowy wokół osi przechodzącej przez jego środek. Moment bezwładności tarczy względem jej osi obrotu wyraża się wzorem 0, 5m * r ^ 2 gdzie m to masa tarczy, a r to jej promień.
4.3 Po pewnym czasie tarcza osiągnęła prędkość kątową o wartości 9 rad/s i przestała się dalej rozpędzać. W pewnym momencie tarczę zaczęto zatrzymywać działając na nią siłą vec F przyłożoną do jej krawędzi o kierunku stycznym do obwodu tarczy w punkcie przyłożenia siły
b) Przyjmując, że wartość siły hamującej vec F wynosiła 20 N, oblicz po jakim czasie tarcza się zatrzyma. (3p)
Na zdjęciu pokazałam, jak próbowałam rozwiązać to zadanie. Dlaczego tym tokiem rozumowania wychodzi niepoprawny wynik? Rozumiem metodę użytą w odpowiedziach, ale nie wiem dlaczego ta też nie działa. Poprawny wynik to E=F/mr.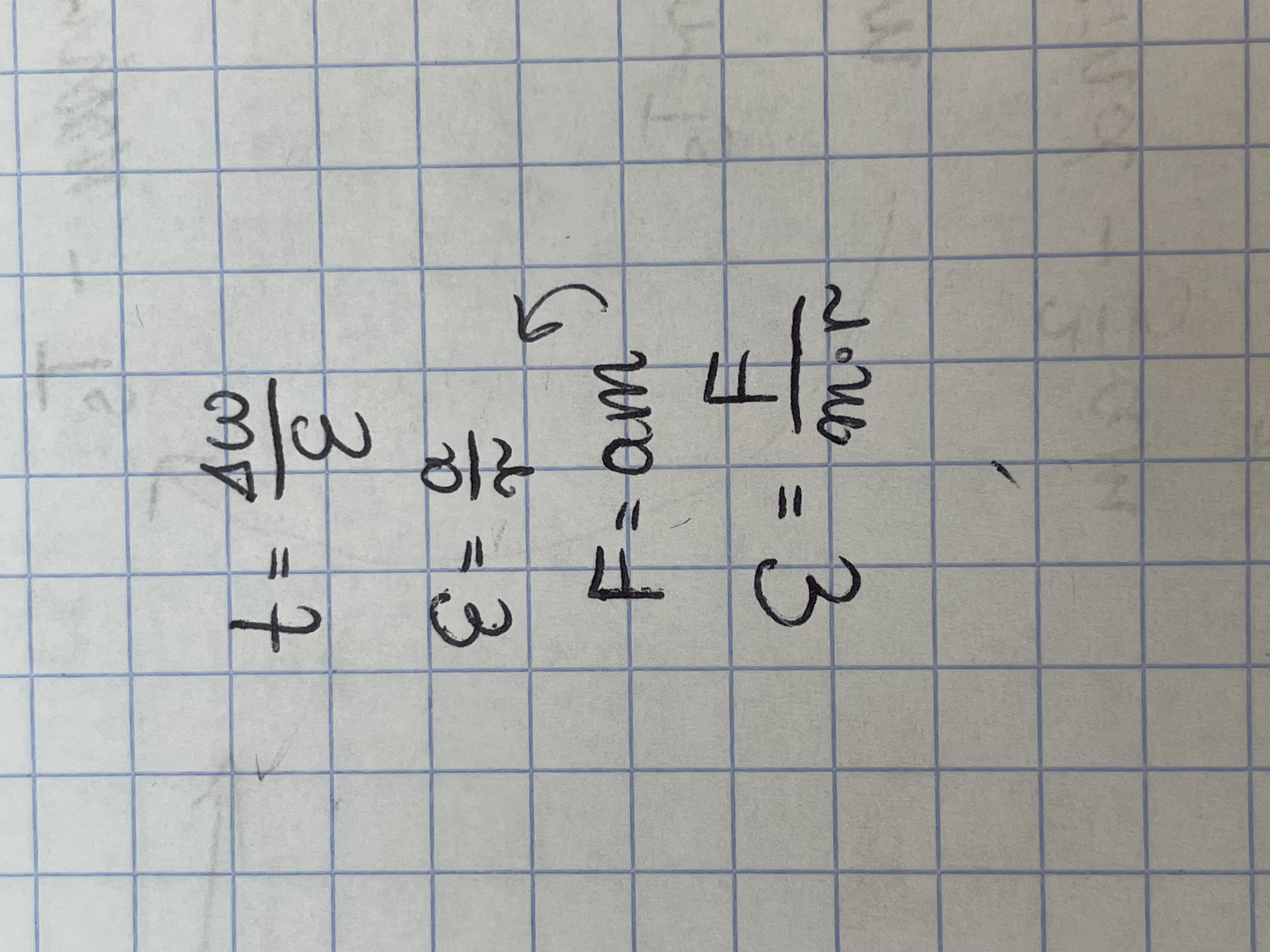
Fizyka zadanie domowe Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nieprawdziwy jest tutaj zapis F = ma, tzn. to równanie jest oczywiście prawdziwe, ale wtedy gdy mówimy o ruchu postępowym (zauważmy, że jest to "treść" II zasady dynamiki Newtona, czyli właśnie w ruchu postępowym). A tutaj tarcza wykonuje tylko ruch obrotowy, więc nie możemy traktować siły F jako takiej, która nadaje tarczy o masie m przyspieszenia liniowego a.