Julka Ch 29 wyśw. 28-10-2025 11:17

2024G.3.1


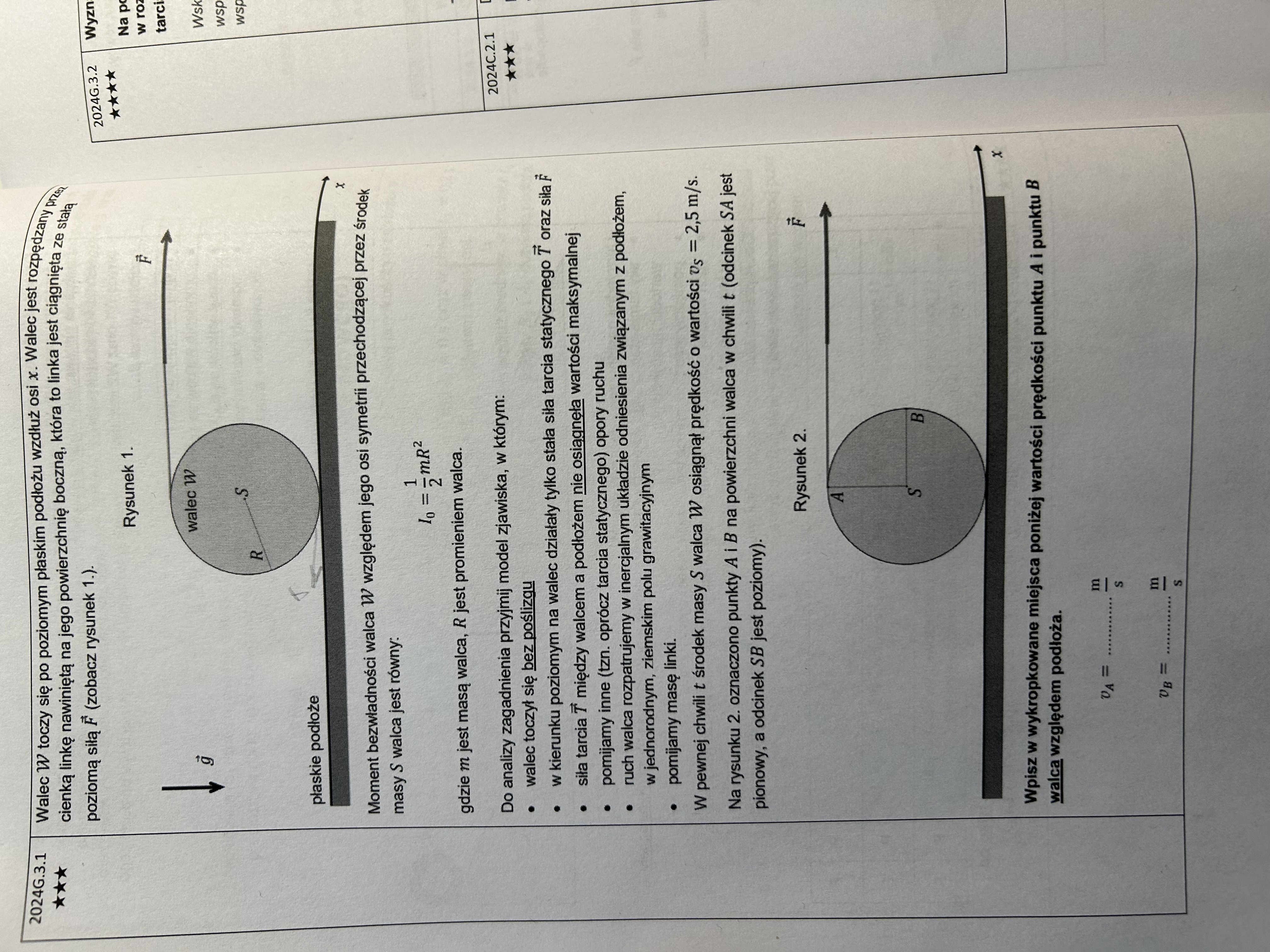
Nie za bardzo rozumiem jak fizycznie to opisać, rozumiem to tak że względem punktu S zachodzi tylko Ek w ruchu obrotowym a dla punktu A i Ek w postępowym i w obrotowym. Rozpisałam już naprawdę przeróżne równania, które wydawało mi się że opisują to zjawisko, ale żadne nie było prawidłowe. Jak w takim razie należy to rozpisać? 
matura zbiór zadań Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula 28-10-2025 12:45

Należy to zrobić dokładnie tak, jak robiliśmy to na zajęciach nr 6, gdy mówiliśmy o prędkościach różnych punktów bryły sztywnej (która toczy się bez poślizgu) względem podłoża. Poniżej zamieszczam screen z tego momentu naszych zajęć:

Należy zauważyć, że w tym zadaniu zarówno punkt A, jak i punkt B (które odpowiadają punktom A i C z naszych zajęć) posiadają pewną prędkość względem podłoża (wektory czerwone), które są złożeniem prędkości tych punktów w ruchu postępowym (wektory niebieskie, które co do wartości są równe wartości wektora prędkości środka masy, czyli w przypadku tego zadania jest to 2,5 m/s) i prędkości tych punktów w ruchu obrotowym względem środka masy (wektory zielone, które z uwagi na fakt, że toczenie jest bez poślizgu, również co do wartości są równe wartości prędkości środka masy, czyli w tym zadaniu 2,5 m/s). To oznacza, że czerwony wektor punktu A, czyli poszukiwana przez nas jego prędkość względem podłoża, ma wartość 2*2,5 m/s = 5 m/s. Z kolei wartość czerwonego wektora punktu B (C z naszych zajęć) możemy obliczyć na przykład z twierdzenia Pitagorasa i wyniesie ona pierw(2)*2,5 m/s.

Julka Ch 28-10-2025 19:37
Już rozumiem, dziękuje bardzo
s.gugula 29-10-2025 12:29

Nie ma sprawy :)