Matura maj 2010
Punkt ( 2,5) A jest jednym z wierzchołków trójkąta równoramiennego , ABC w którym AC=BC. Pole tego trójkąta jest równe 15. Bok BC jest zawarty w prostej o równaniu y=ax+1. Oblicz współrzędne wierzchołka c
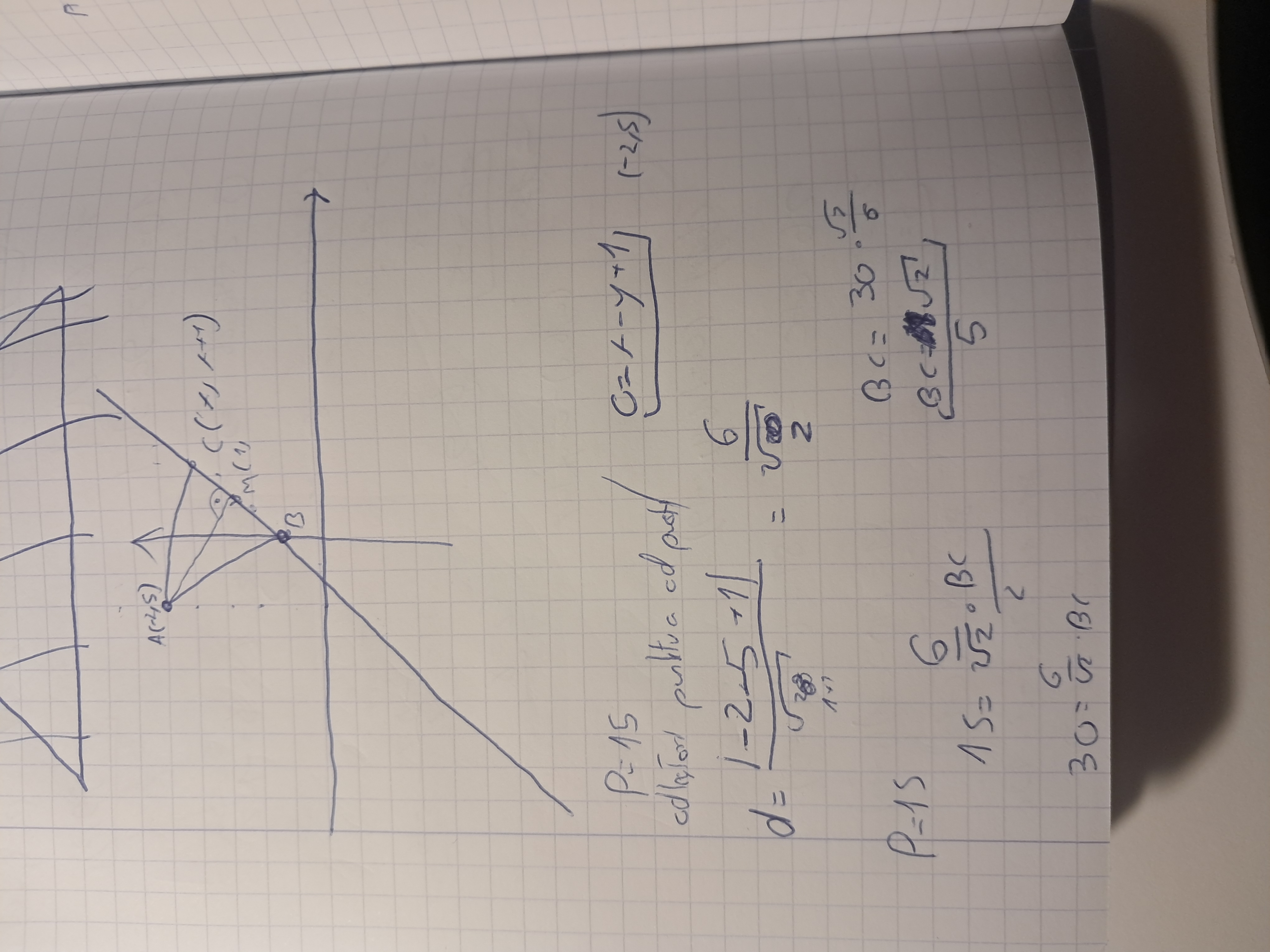
Nie moge znaleść błedu w swoim rozwiązaniu. Wyliczam odległość punktu a od prostej czyli wysokość( 3√2). Potem z pola wyliczam odległość trójkąta BC= 5√2. Dalej licze prostą AM(m to punk wysokości na podstawię) z informacji że jest prostopadłe do prostej Boku BC i zawiera punkt A. Liczę punkt wspólny M(1,2). M jest środkiem z własności trójkąta równoramiennego stąd wiem że MC=5√2 / 2 i tu z wzoru na odcinek i z informacji że C (x,x+1) wychodzi mi totalnie inny wynik.
Również gdy próbowałem narysować ta sytuację w Geogebra z wynikami odpowiedzi do matury pole trójkąta jest całkowicie inne oraz długość boku BC, z czego to wynika 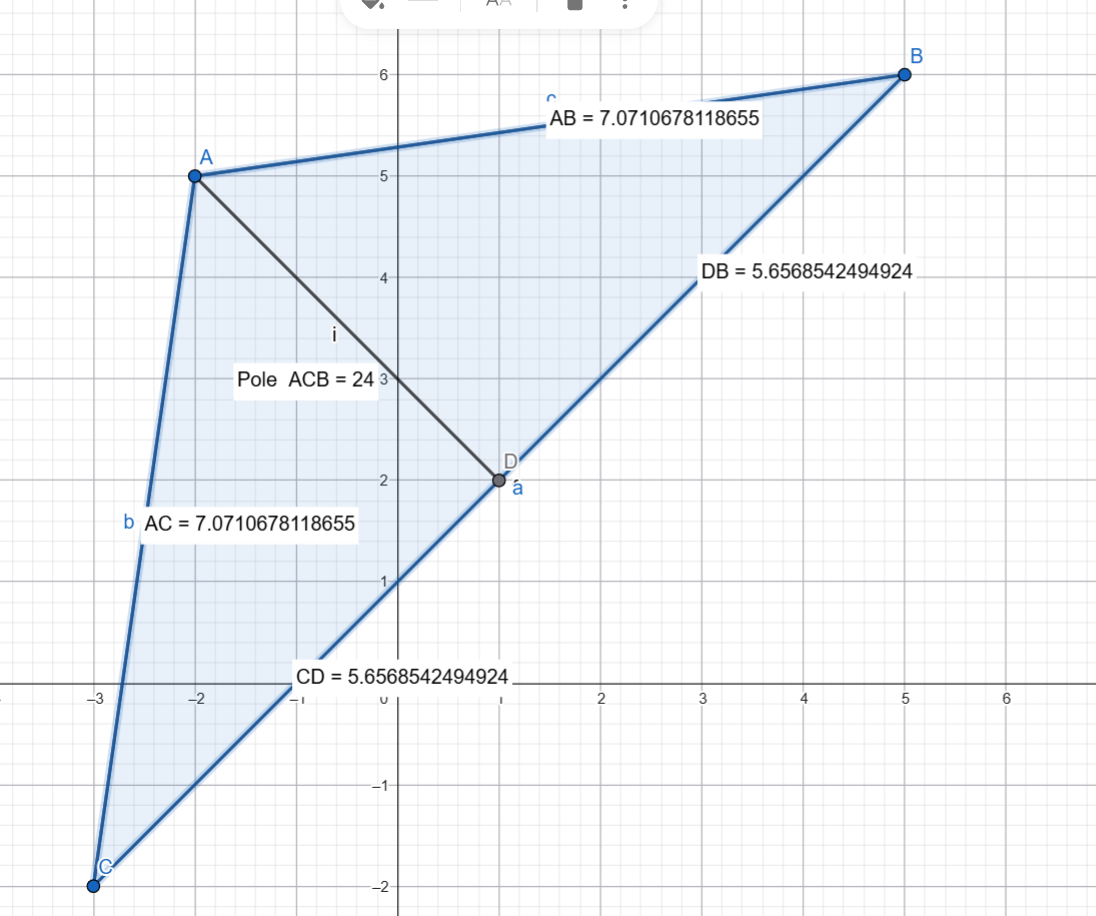
Matura Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Gdzie znajduje się odpowiedź?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Licząc delte z ostatniego równania ( 2x²-4x+2-5sqr2) x wyszło mi bardzo dziwne( na innej kartce liczyłem bo mi się miejsce skonczyło) i x który wyszedł był nie zgodny z odpowiedziami
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tylko ramiona to BC oraz AC, a nie AC, BC
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

Zaprezentuj swoje obliczenia.