zad 12 arkusz V
Dane są okręgi x^2 -4x + y^2 -6y+9=0 i x^2 -2a+y^2+4y+a^2=21. Wyznacz wszystkie wartości parametru a, dla któych te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki
Gdzie robie błąd?
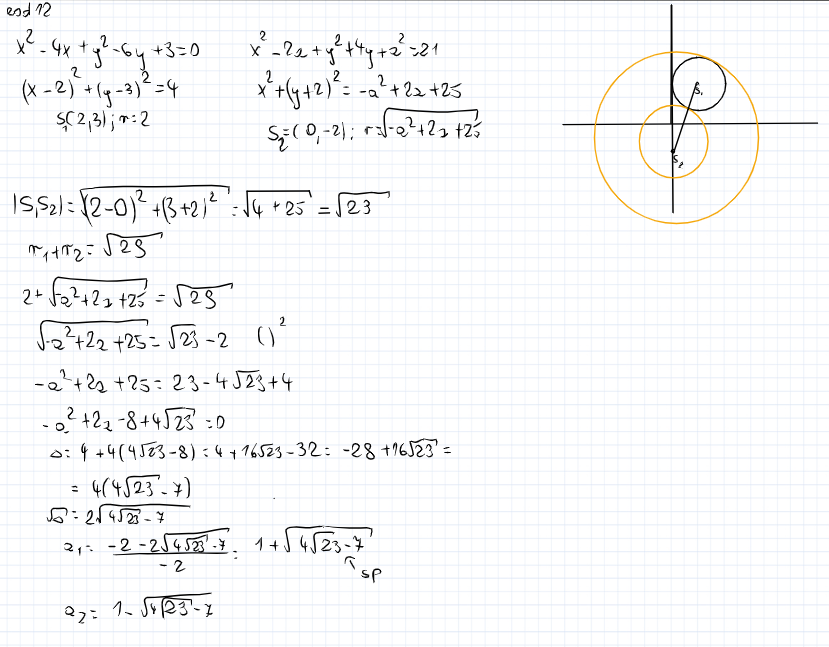
matematyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Odpowiedzi ci wyszły takie jak w kryteriach?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Odpowiedzi ci wyszły takie jak w kryteriach?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
2- pierwiastek z 6 i 2+ pierwiastek z 6. Tobie też?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Mi takie cuś wyszło 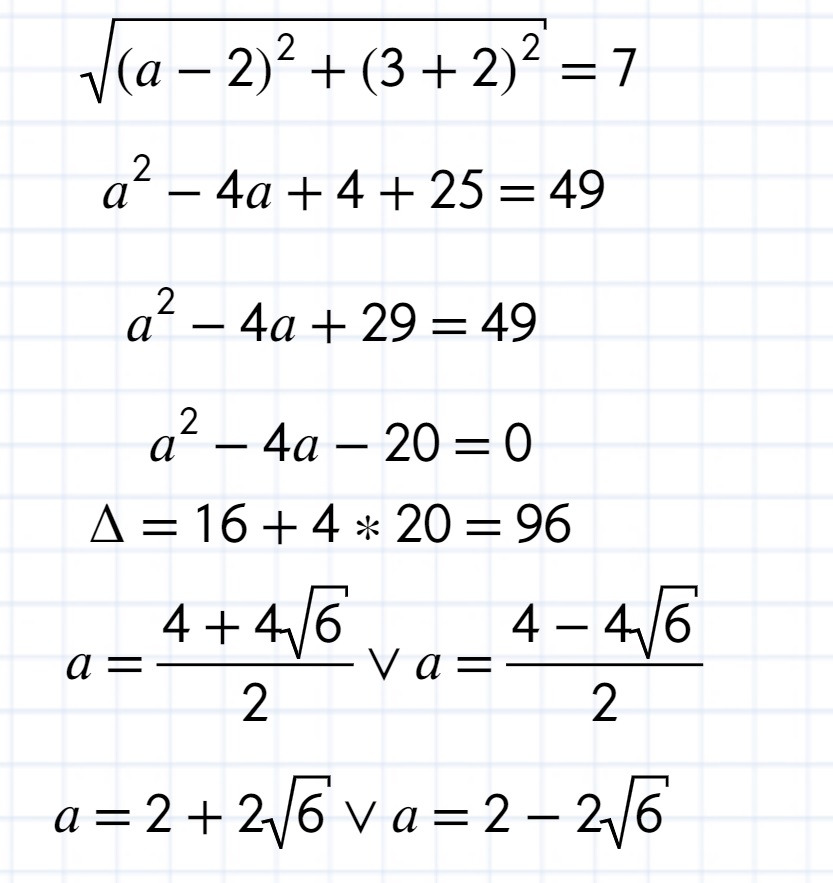
Daj znać czy moja odpowiedź się zgadza, czy to ja się pomyliłem hah
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
tak tak, zle napisałem komentarz wyzej tak samo mi wyszlo jak tobie
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A zadanie 15 z 5 arkusza zrobiłeś?
Wyszła mi prawidłowa długość krawędzi podstawy ale wysokość nie gra.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dokładnie, czyli znowu błąd w kryteriach ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
tak mi sie wydaje. w Zad 8 z arkusza V tez jest chyba blad
https://forum.szkolamaturzystow.pl/wpis/1616707985-arkusz-5-zadanie-8?notif=komentarzdodany
Potwierdz jeśli możesz bo jeśli tak to bede sobie musiał zmienić wynik w pracy domowej
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
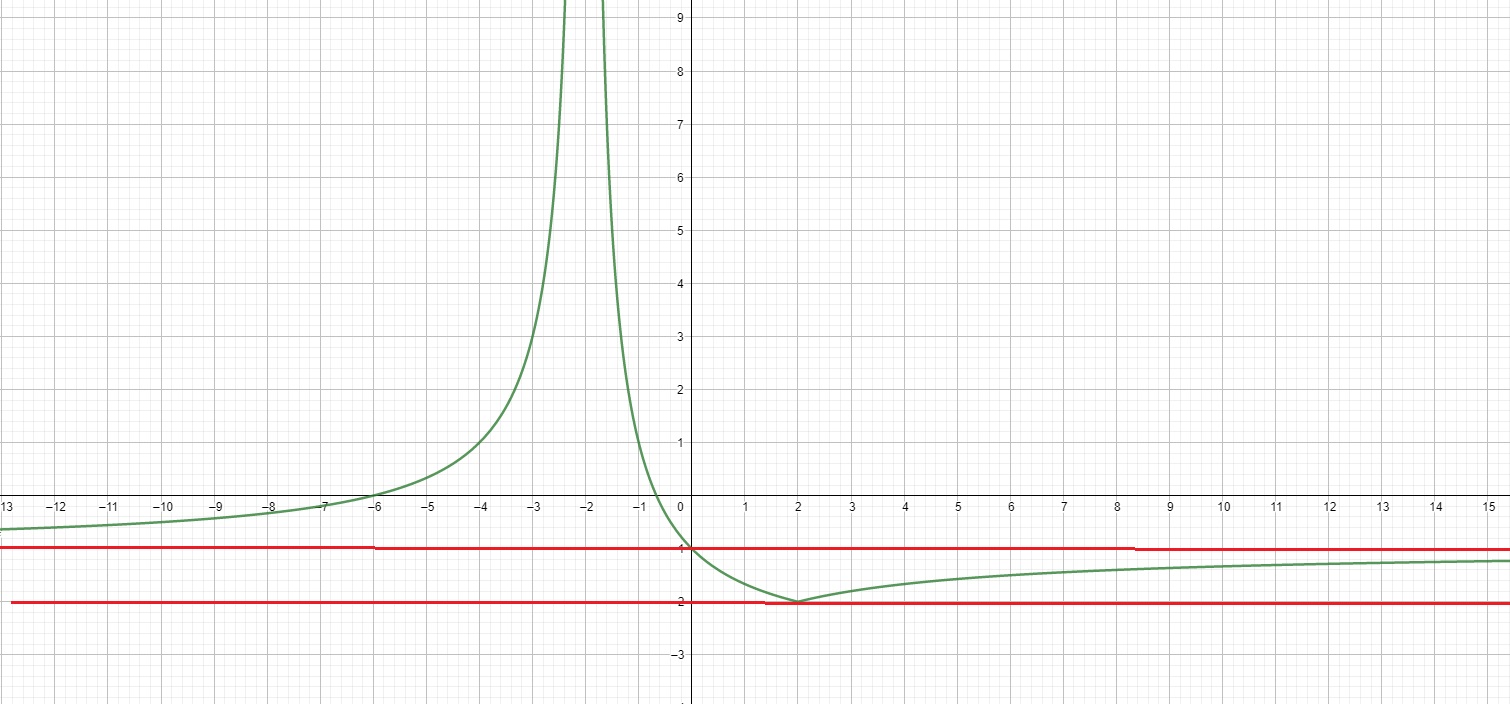
Oczywiście, że jest błąd, w geogebrze od razu widać, że dla a=-1 i a=-2 mamy jedno rozwiązanie.
Zawsze możesz podstawić sobie to ,,a'' i rozwiązać równanie, sporo tych błędów.
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
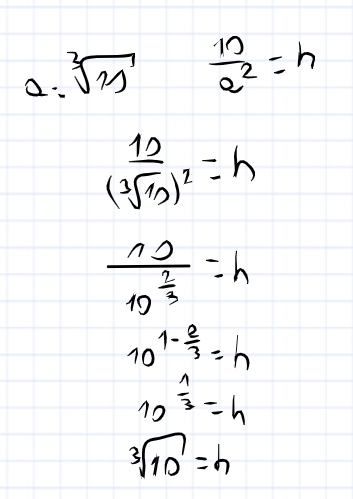
Napisałem do Pana Jarosińskiego okazuje się ze w poleceniu przy drugim okręgu przy -2a powinno byc -2ax