Zad 10 arkusz XVI

Mogę prosić o rozpisanie. Szczególnie zależy mi na dojsciu do sq = sr
Matematyka Dodaj post do ulubionych Poproś o pomoc
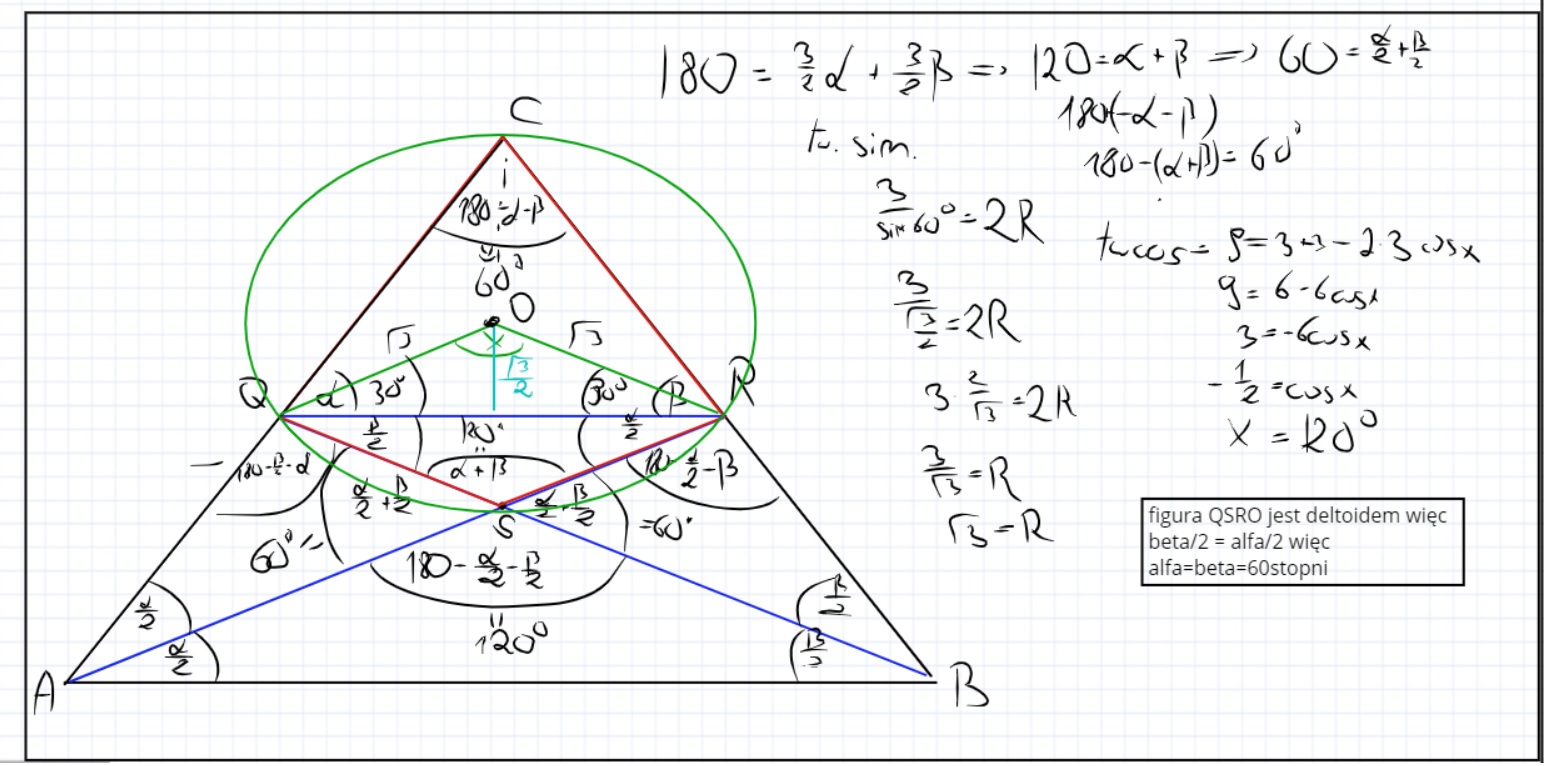 myślę, że z resztą zadania sobie poradzisz, a jeśli nie to mogę ci je rozpisać.
myślę, że z resztą zadania sobie poradzisz, a jeśli nie to mogę ci je rozpisać.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Lelum Polelum
Mógłbyś wyjaśnić skąd biorą się kąty SQR oraz SRQ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jak będziesz sobie pokolei wypisywać kąty to do tego dojdziesz, muszą tak być takie kąty ponieważ tylko wtedy będzie możliwe dopełnienie do 180 stopni przy danych ścianach.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dochodzę do tego etapu. Co dalej? 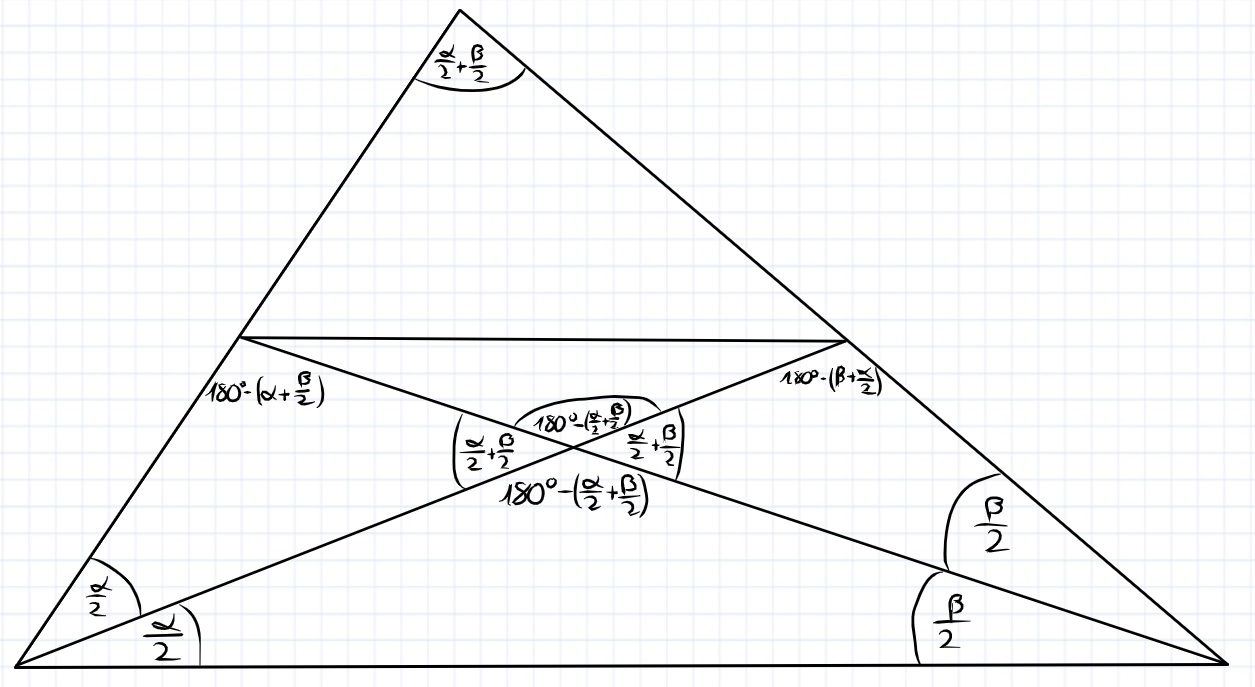
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Moim zdaniem twoje uzasadnienie jest błędne.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Trójkąt QRO i QRS są przystające ponieważ mają takie same pole taka sama wysokość mają identyczny kąt na przeciwko podstawy i dzielą jedna podstawowe.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Znaczy gdybym widział całość twojego rozwiązania to może potrafiłbym ocenić czy jest ono poprawne czy nie natomiast póki co wszystkie twoje wnioski są jak dla mnie dopasowane do odpowiedzi i nie koniecznie mają zaplecze. Nie rozumiem dlaczego uważasz że odległość którą zaznaczyłeś na niebisko (pierwiastke z trzech przez 2) jeżeli przeciągniemy ją do punktu S to będzie ona dalej wysokością, nie wiesz czy tak jest!
Z rysunku wygląda jakby tak było ( prawdopodobnie tak jest ) ale nie jesteś w stanie stwierdzic czy tak jest czy nie.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie wykluczam że się mylę, ale chyba przy wspólnej podstawie to dalej musi być wysokość, tak mi się przynjamniej wydaje, bo musi z jeden i z drugiej strony przechodzić pod tym samym kątem a na końcu i tak dąży do wierzchołka tego trójkąta.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
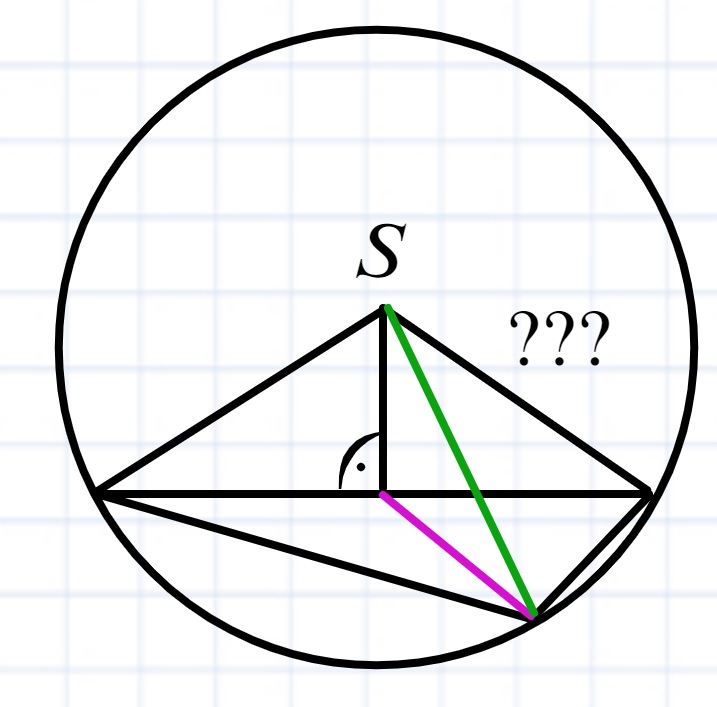
Nie mówię, prawdopodobnie w tym zadaniu tak będzie!
Ale przynajmniej w mojej ocenie nie możemy wysnuć takich wniosków tylko na podstawie rysunku. Być może jesteś mi w stanie udowodnić że promień przecina podstawę pod kątem prostym i trafia idealnie do wierzchołka. Jak mi to udowodnisz to super bo wtedy jest po zadaniu i może zrozumiem to zadanie, ale póki co moim zdaniem nie można wysnuć tego wniosku.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Poprosiłem Pana Jarosińskiego aby zajrzał tutaj: https://forum.szkolamaturzystow.pl/wpis/1618057694-arkusz-xvi-zad-10
Możesz śledzić ten temat, moim zdaniem czegoś brakuje w tym zadaniu, być może ja czegoś nie widzę, absolutnie tego nie wykluczam, ale już na tyle sposobów próbowałem dojść do rozwiązania i cały czas coś nie trzyma się czegoś ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A masz może gdzieś kryteria do tego zadania? Bardzo jetsem ciekawy jak to tam wygląda.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

Próbowałem rozwiązać to zadanie sposobem z kryteriów, ale jest ono dla mnie również nie zrozumiałe, jakby ci się udało zrobić to sposobem z kryteriów to podziel się :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jutro spróbuję to zrobić, i w sumie teraz zauważyłem że chyba kąty obu trójkątów nie są takie same na twoim rysunku.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ok tylko nawet jakby był ten kąt równy i nawet jakby wyglądało że tak jest to tak czy siak musisz to uzasadnić.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A napisanie że wysokość jest jednocześnie dwusieczna w jednym i drugim trójkącie by nie starczyło? (Musi tak być bo są równoramienne) bo jakoś inaczej będzie ciężko to udowodnić
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To już chyba by wystarczyło, ale skąd wiesz że tak jest?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A dlaczego uważasz że SQ=SR?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W sumie to na łuku QS oparty jest kat alfa/2 i jest na nim oparta połowa kąta x więc alfa/2 to 1/4x z czego wynika że to 30 stopni a skoro ten kąt jest równy 30 stopni to drugi też musi być równy 30 stopni żeby trójkąt miał łącznie 180. Ale w sumie to jets bez sensu bo w sumie nwm czy to na pewno połowa kąta x. Mój błąd.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Rozwiązanie wyszło łatwiejsze niż myślałem, a wystarczyło sobie pociągnąć kolejną dwusieczną, w każdym razie dzięki za rozpisanie poprawnego rozwiązania.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
