Kłaczkow 7.85

miałam ten sam problem, tu trzeba sie doczytać że mają być 2 karty w INNYM KOLORZE, wiec w jednym i tym samym, a nie w INNYCH KOLORACH, wtedy chyba byłoby więcej możliwości

A potrafisz u mnie znaleźć błąd w rozumowaniu w podpunkcie c? Bo tutaj już kolory pozostałych są dowolne.

Zgadza się. To zadanie mogłoby być lepiej dopracowane. Czy jeszcze coś należy tu wyjaśnić? Ktoś zgłosił prośbę o pomoc

Tak, prosiłbym o wyjaśnienie podpunktu c, bo nie rozumiem jaki mam błąd.

1. Zliczasz zbyt dużo przypadków.

Przeanalizuj proszę https://forum.szkolamaturzystow.pl/wpis/1616487618-785-c-klaczkow

Gdzie rozwiązano to zliczając po kolei każdy przypadek.

Problemem jest to że zliczasz dodatkowe przypadki, przykładowo w pierwszej częsci losujesz 2 kart sposród 13 a następnie 2 sposrod 39, w zaden sposob nie zabezpieczasz w kolejnym 13 po 3* 39 po 1 aby nie powtórzyć tych samych przypadków.

przypadki „2 w jednym kolorze” i „2 w innym kolorze” nachodzą na siebie (podobnie w przypadku „2 w jednym kolorze” i „3 w innym kolorze” itd.). Zdarzenia, które miały być „rozłączne”, w rzeczywistości wcale rozłączne nie są:

Możesz np. wziąć 2 karty kier i 2 karty karo. Taki układ zostanie policzony dwukrotnie:

raz jako „2 karty z koloru kier” plus „2 karty z pozostałych 39, z czego akurat 2 karo”,

drugi raz jako „2 karty z koloru karo” plus „2 karty z pozostałych 39, z czego akurat 2 kier”.

Przykładowo w ten sposób obliczylbym przypadek z trzema kartami tego samego koloru.

To z 2 przypadku wychodzi mi 133848 sposobów a 3 przypadek mam taki: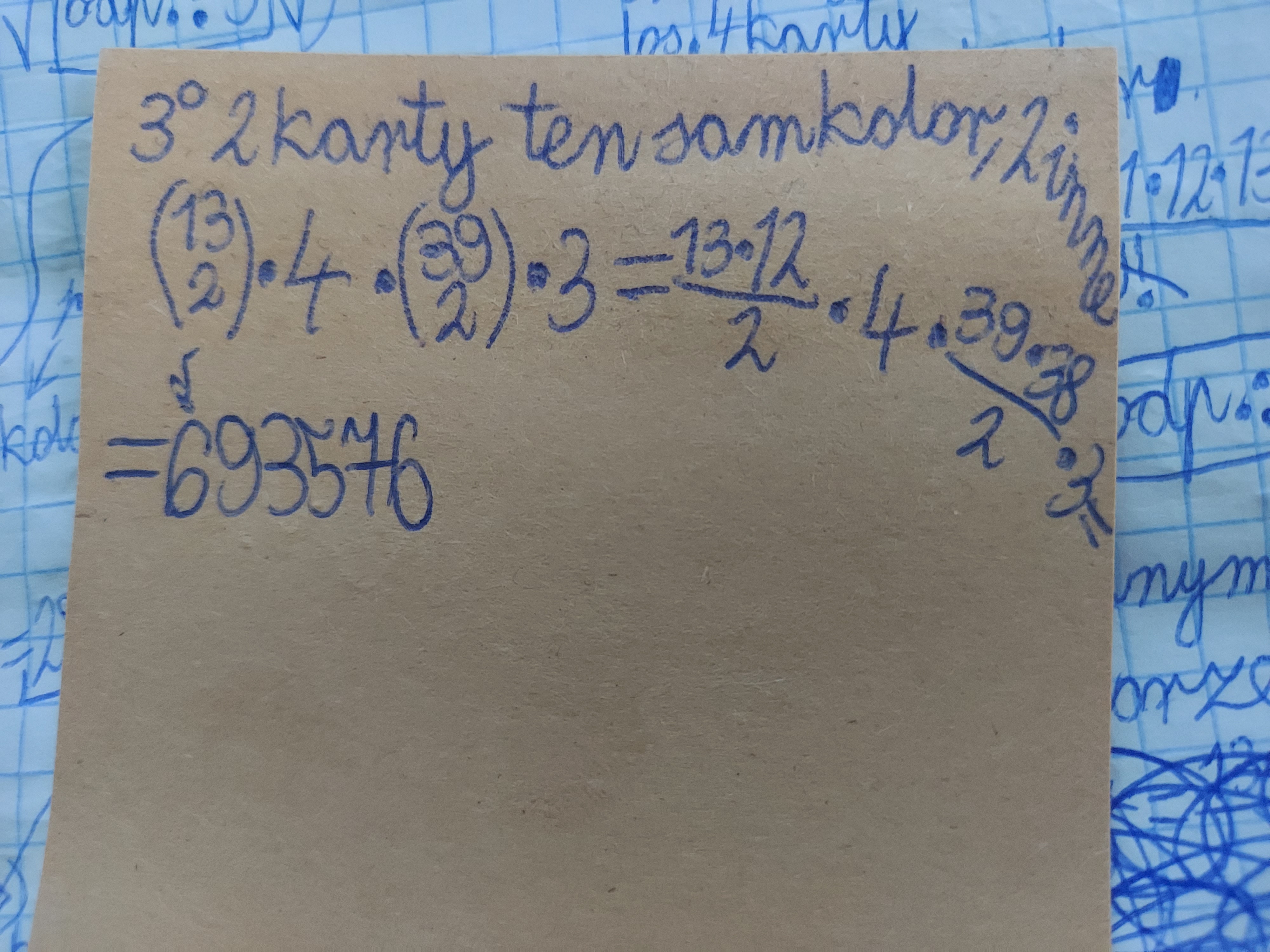

Od lewej: wybór 2 kart tego samego koloru*4kolory*wybór 2 kart pozostałych*3 pozostałe kolory

I z samego tego przypadku wychodzi mi 693576 co jest większe nie odpowiedź.

Proszę rozpisz jeszcze raz wszystkie przypadki na jednej kartce jeden pod drugim, pod każdym czynnikiem napisz rozumowanie - co wybierasz z czego po ile i dlaczego.

W każdym z przypadków zasada jest taka sama:

1.czynnik to wybór kart tego samego koloru

2.czynnik to wybór koloru dla kart w tym samym kolorze 

3.czynnik to wybór kart pozostałych 

4.czynnik to wybór koloru dla kart pozostałych 

Po raz kolejny zliczasz te same przypadki wielokrotnie. 

Przykładowo w przypadku 2:

3 karty ten sam kolor; 1 inna: 
Pierw wybierasz 3 karty spośród 13 danego koloru. 

Musisz pierw wybrać kolor: 

Zatem mnożymy to przez 4, ponieważ mamy 4 kolory. 
Następnie z pozostałych 39 wybieramy jedną kartę i mamy już uwzględnione wszystkie możliwości. 

W jakim celu dodatkowo to mnożyć * 3  - nie ma to tutaj żadnego sensu. 

No chcę mnożyć to razy 3, aby czwarta karta była innego koloru niż trzy poprzednie.

Tak jak wspomniałem w poprzednim poście w którym zadałeś pytanie. Jeżeli wybieramy pierw karty spośród danego koloru, a następnie spośród kart innego TO W NICH już nie ma tego pierwszego koloru.