2020.8.3
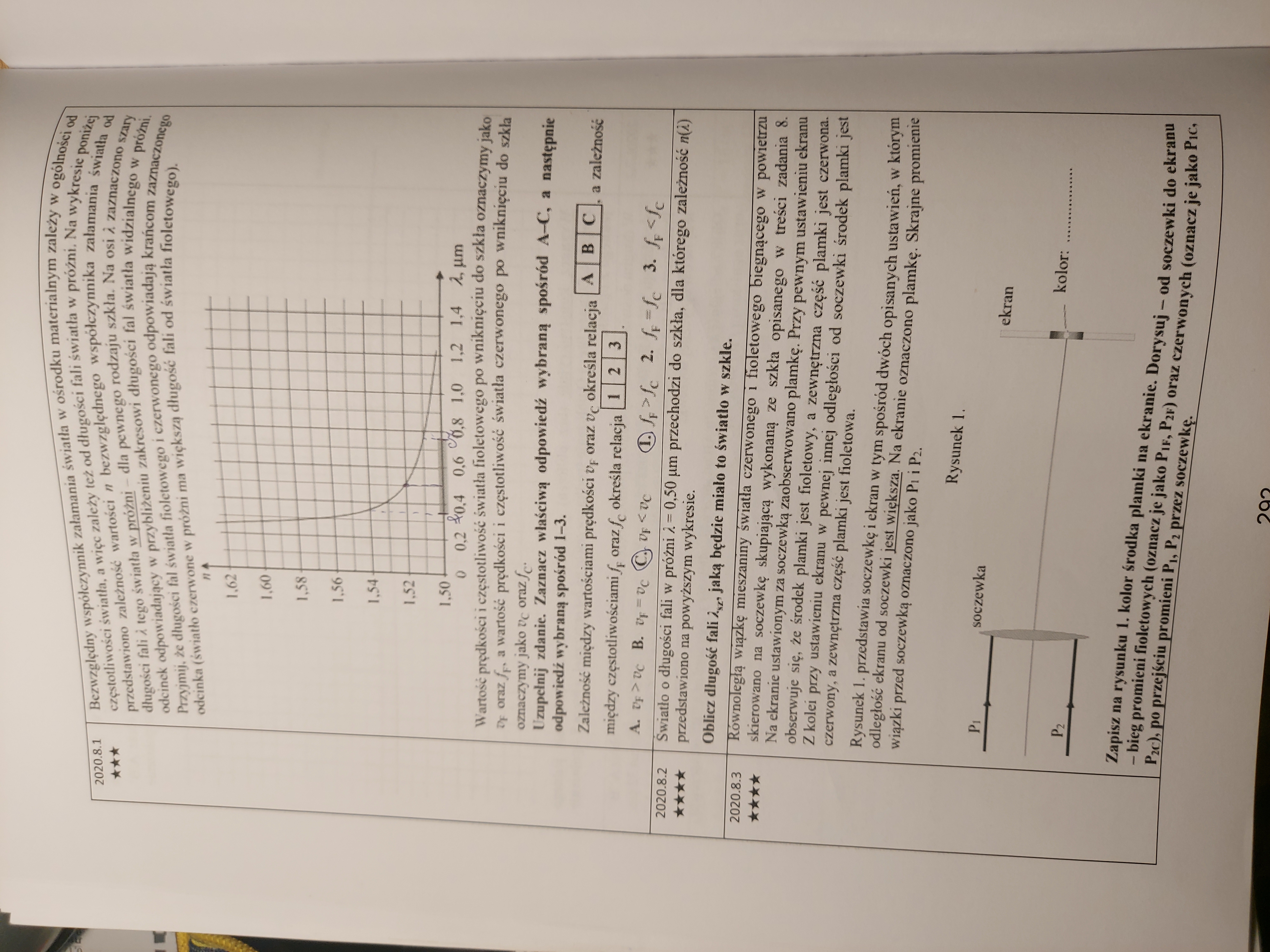
Nie mam pojęcia jak zrobić ten podpunkt :/
Fizyka optyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
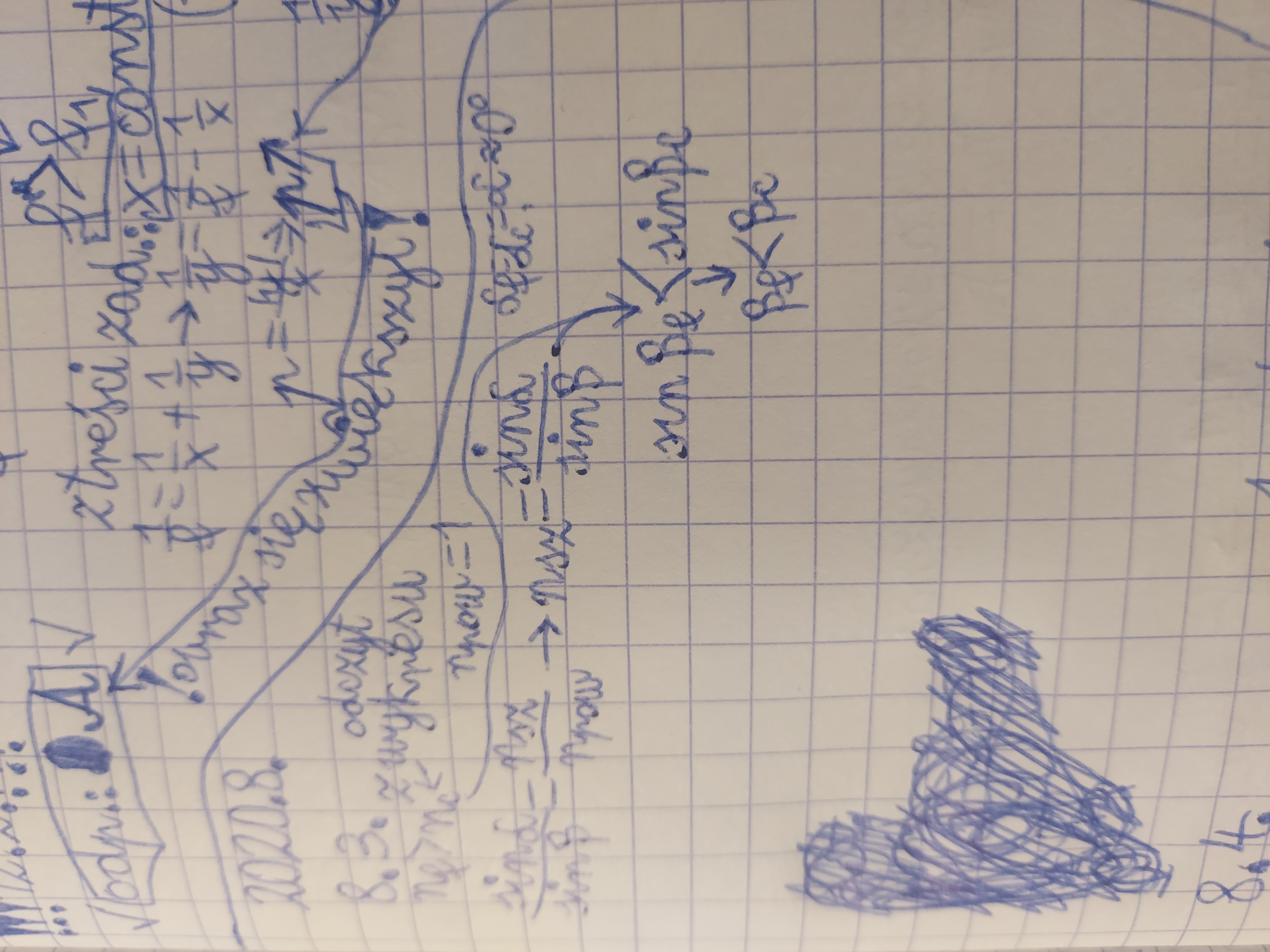
Z tego co zrozumiałem to w obliczeniach wyglądało by to jak powyżej. Ale czy kąt padania na soczewkę nie będzie równy albo zbliżony do 0 stopni? Czy też właśnie będzie równy 90 stopni? Bo nie wiem gdzie tutaj zaznaczyć normalną.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wygląda ok. Tak, ten kąt padania na soczewkę będzie bliski 0 stopni (ale nieco większy niż 0).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli normalna w soczewce będzie w przybliżeniu szła wzdłuż promieni P1 i P2?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W przybliżeniu tak, ale między nią a tym promieniem (czy to P1 albo P2) będzie właśnie jednak jakiś niewielki kąt.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chwila, ale skoro normalna jest w przybliżeniu liniami P1 i P2 to skoro wyszło, że beta_fiol < beta_czerw to promień czerwony bardziej "ugina się", więc z tego mi wynika, że dalej powinny się przeciąć promienie fioletowe.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ale to jest tylok tak w przybliżeniu - w rzeczywistości te normalne to nie P1 (czy tam P2). I w rzeczywistości dochodzi przy przejściu światła przez soczewkę do jego dwukrotnego załamania. Ale np. dla promieni górnych to wygląda dokładnie analogicznie do tego jak to jest dla pryzmatu (co omawialiśmy na koniec zajęć nr 22). Wspomniałem o tym również w innym temacie na naszym forum, więc polecam tam zerknąć (tam faktycznie wychodziło, że promień czerwony leciał "wyżej", tzn. dalej od osi optycznej niż fioletowy): https://forum.szkolamaturzystow.pl/wpis/1741807838-zad202083
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli kolokwialnie rzecz ujmując to tutaj normalna pochodząca od P1 przechodzi jakoś mniej więcej pod P1F? Czyli w tego typu zadaniach warto zapamiętać, że zawsze sytuacja wygląda identycznie jak w pryzmacie?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ta normalna do prawej powierzchni soczewki leży akurat nad promieniem P1F (po prawej stronie soczewki) - znów zgodnie z tym co na zajęciach w tym zadaniu z pryzmatem. I tak, można to sobie tak zapamiętać (o ile układ oczywiście będzie analogiczny).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Leży ona nad oboma tymi promieniami. A te obliczenia były robione dla pierwszego załamania, czyli wejścia promienia z powietrza do szkła soczewki. Dlatego też zdecydowanie zachęcam do zajrzenia do tego zadania z pryzmatem, bo tam analizowane są oba przejścia i faktycznie uzyskujemy to co tutaj, czyli, że promień czerwony idzie "dalej" od osi optycznej niż fioletowy.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Znów należy pamiętać, że mamy dwa momenty załamania. Pierwszy gdy światło przechodzi z powietrza do soczewki - wówczas beta_c > beta_f, a oba te promienie leżą nad normalną. Następnie mamy drugie załamanie, gdy światło wychodzi z soczewki do powietrza - wówczas faktycznie beta_f > beta_c, a oba promienie leżą pod normalną. Oba te efekty dają ostatecznie to, że promień czerwony biegnie dalej od osi optycznej niż fioletowy.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale patrząc na to, że sytuacja jest analogiczna do tej z pryzmatem, a tam promień 2 razy załamywał się w tę samą stronę to tutaj chyba nie powinno być zmiany znaku nierówności przy kątach (tzn. jeśli dla przejścia powietrze-soczewka wyszło beta_1f>beta_1c to dla przejścia soczewka-powietrze powinno wyjść także beta_2f>beta_2c).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No właśnie zgodnie z prawem załamania będzie ta zmiana :) Raz współczynnik załamania światła dla szkła jest w liczniku, a raz w mianowniku ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A racja, pomyliło mi się. To właściwie dlaczego w pryzmacie 2 razy promień załamuje się w dół? Chyba mówiliśmy wtedy na to "od normalnej".
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No cóż, wynika to po prostu z prawa załamania, nie wiem co tu w zasadzie więcej można dodać ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Bo jakoś nie mogę zauważyć trochę tej analogii między pryzmatem i soczewką. Czy można to po prostu zrozumieć tak, że w soczewce zawsze będzie to wyglądało tak jak w pryzmacie? Czy np. dotyczy to tylko soczewki skupiającej?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Analogia jest taka jak zobrazowałem to w prymitywny sposób poniżej ;) można sobie wyobrazić, że pryzmat jest górną częścią soczewki skupiającej.
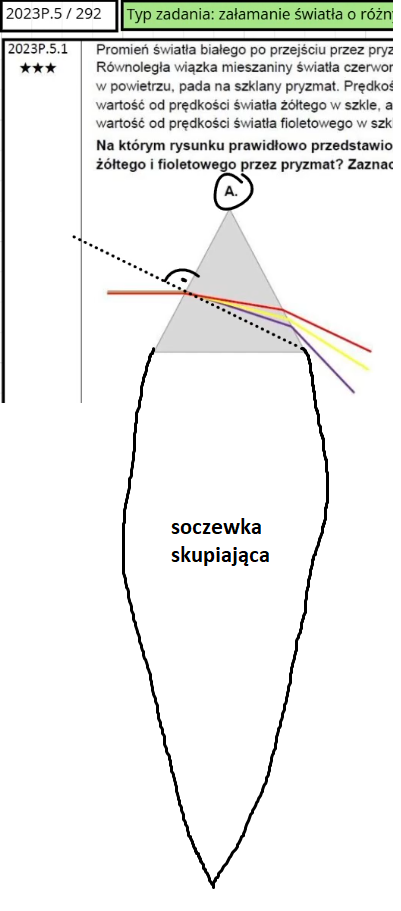
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
O teraz to ma sens. A gdyby była mowa o soczewce rozpraszającej to analogicznie poprawną odpowiedzią byłoby "E" w tamtym zadaniu?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tamto zadanie to jest zadanie z pryzmatem a nie soczewką, więc to co innego ;) A w tym przypadku to zadanie z soczewką rozpraszającą nie ma sensu, bo po przejściu przez soczewkę te promienie nie skupiałyby się nigdzie, tylko rozpraszało. Ale jeśli bardzo chciałbyś powiązać bieg promieni świetlnych po przejściu przez soczewkę rozpraszającą z tym jak to wygląda w przypadku pryzmatu, to patrząc na typowy kształt soczewki rozpraszającej należałoby odwrócić pryzmat "do góry nogami".
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No i właśnie wtedy nie wyglądałoby to podobnie jak w odpowiedzi E w tamtym zadaniu?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jak odwrócisz pryzmat z przypadku A do góry nogami to promienie biegną "tak jak" w F, a nie E ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
I wtedy F symbolizuje rozszczepienie promieni świetlnych dla soczewki rozpraszającej tak?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wiąże się to z zadaniem, które robiliśmy pod koniec tych zajęć nr 22 z pryzmatem. Otóż wszystkim rządzi tu różna wartość n dla światła czerwonego i fioletowego. Ponieważ n_f > n_c, to np. przy przejściu wiązki światła z powietrza do szkła (wejście do soczewki) zgodnie z prawem załamania, kąt załamania beta będzie większy dla światła czerwonego niż dla fioletowego (czyli światła czerwone będzie mocniej odchylone od normalnej niż światło fioletowe). To będzie oznaczało, że ostatecznie wiązka światła czerwonego po przejściu przez soczewkę będzie szła "dalej" od osi optycznej niż wiązka światła fioletowego, toteż przecięcie się wiązek światła czerwonego na osi optycznej nastąpi w dalszej odległości od soczewki niż ma to miejsce dla wiązek światła fioletowego. Stąd w tym przypadku środkowa plamka na ekranie jest własnie czerwona (bo jest on ustawiony dalej zgodnie z treścią). Dobrze oddaje to rysunek podany przez CKE jako rozwiązanie, wrzucam go poniżej: