ZZ.157
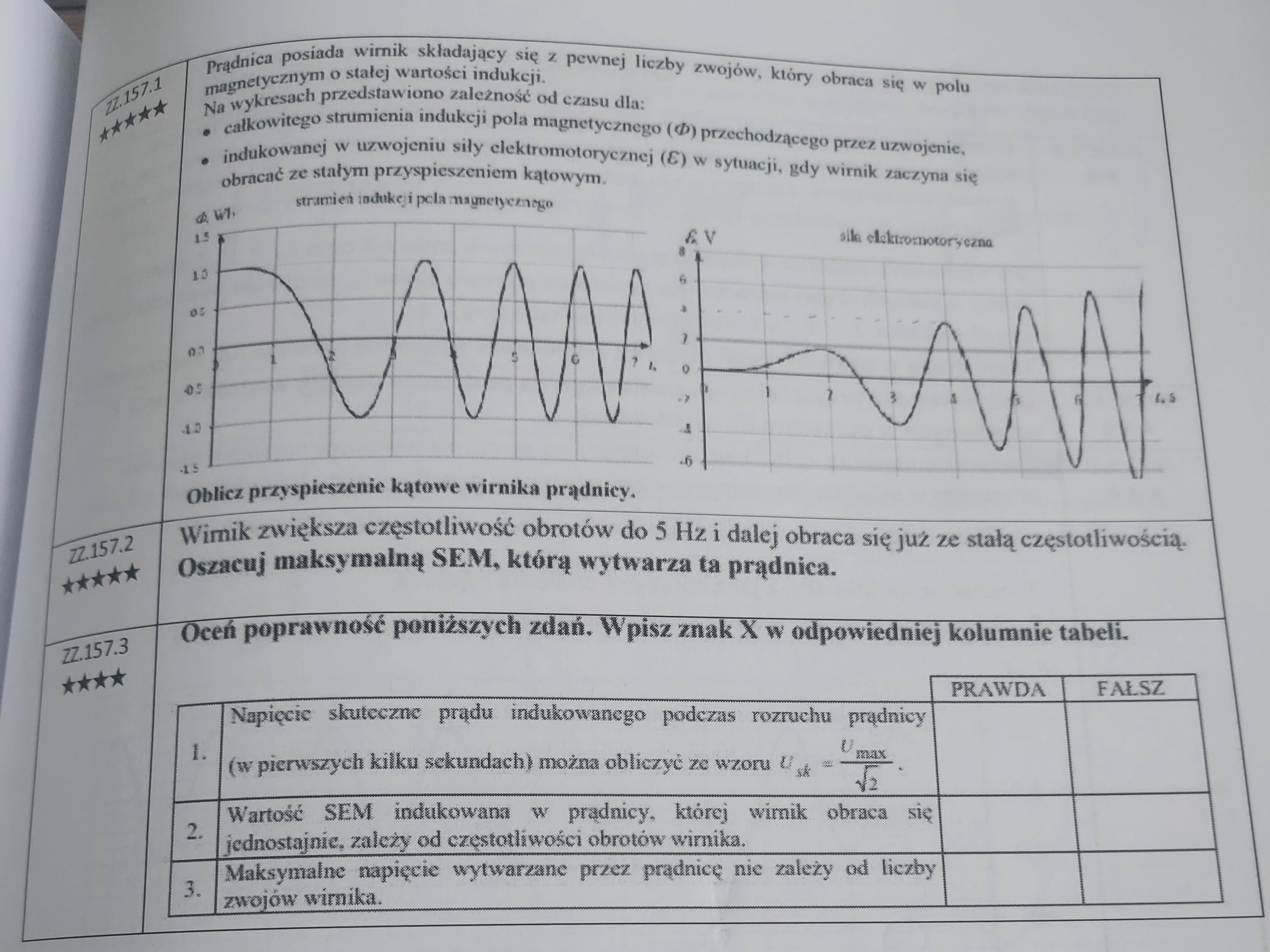

157.1.: Jak obliczyć to przyspieszenie kątowe? Ja doszedłem do jakiejś sprzeczności.
157.2.: Jak obliczyć Umax nie mając danej liczby zwojów?
157.3.: 1-czy to zdanie jest fałszywe, dlatego że okres nie jest stały?
Pytanie ogólne: Czy tutaj mamy do czynienia z rezonansem? Bo wykres wydaje mi się podobny do drgań tłumionych/wymuszonych.
Fizyka elektromagnetyzm Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
157.1.: A skąd pewność, że omega0=0? Bo pełny wzór chyba jest taki: alfa=omega0*t+(epsilon*t^2)/2
I wszędzie na forum widzę rozwiązania na podstawie powyższego wzoru, a pisał Pan, że da się to także zrobić ze wzoru epsilon=delta omega/delta t. W jaki sposób można to obliczyć?
157.2.: W jednym z tematów pisał Pan także, że odpowiedź Umax=31,4V także byłaby ok. Z tego co widzę to u mnie jeśli bym przyjął liczbę zwojów N=1 to właśnie taki wyjdzie wynik. Z czego to wynika, że dla pewnej ilości zwojów wynik się zgadza i czy to przypadek?
157.3.1.: To ja bym napisał, że faza początkowa=0, bo dla t=0 jest epsilon=0, ale rozumiem, że sam fakt "niestałości" okresu jest wystarczającym powodem.
No to może są to jakby drgania wymuszone?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To, że początkowa omega jest zerowa możemy wywnioskować z faktu, że na początku indukowane napięcie było zerowe, czyli prądnica nie obracała się.
Co do obliczenia, że epsilon = delta omeaga / deltat, to moglibyśmy próbować oszacować jaka jest wartość omega p. w pewnym momencie w czasie (jako 2*pi/T, czyli np. w 5 sekundzie możemy oszacować, że omega to jest ok. 2*pi/1,5 s) i potem oszacować tę omegę w innym czasie i w liczniku wrzucić różnicę tych omeg, a w mianowniku różnicę tych czasów, dla których ją obliczyliśmy i dostaniemy jakieś oszacowanie na epsilon, ale powiedzmy sobie szczerze, że ono będzie dość mocno niedokładne ;) no ale jest to jakaś próba szacowania.
157.2: Ja w tym temacie napisałem nawet, że to jest ok, jeśli przyjmiemy, że ten maksymalny strumień 1 Wb to jest wartość z już uwzględnioną liczbą zwojów - to nie musi być N = 1, ważne, że N*B*S = 1 Wb.
157.3 - ok, ale nie widzę jakie znaczenie ma tu faza początkowa ;)
Nie są to drgania wymuszone, to jest po prostu prądnica, która porusza się ruchem przyspieszonym i tyle ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
157.1.: To np dla dwóch pierwszych okresów wychodzi epsilon=1,,2 rad/s^2. Czy taki wynik by uznano?
157.2.:
Mi wychodzi taki wzór i jak się wstawi N=1 to wtedy Umax=31,4V.
157.3.: Ma znaczenie dla sinusa kąta, ale chyba czas trwania jednego okresu nie jest stały to w ogóle nie trzeba tego rozważać z tego co zrozumiałem.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ok, chodziło mi o to, że być może to Fi, które jest na wykresie to tak naprawdę nie jest B*S, tylko właśnie B*S*N (czyli już przemnożone przez liczbę ramek) i wtedy nie musi to być koniecznie jedna ramka.
A faza początkowa ma znaczenie jak sama nazwa wskazuje na początkową wartość tego kąta, a nie ma w istocie żadnego wpływu np. na okres, więc ona faktycznie nie gra tu roli.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
157.1.: Czyli ten wynik 1,2 rad/s^2 byłby ok?
157.3.: Ale to na dzisiejszej maturze by doprecyzowali prawda? Gdyby chodziło o to, że fi = B*S*N. Bo to z treści niezbyt wynika.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
157.1: Nie bardzo mogę zlokalizować miejsce, w którym doszedłeś do takiego wyniku, ale takie oszacowanie w istocie byłoby niezłe ;)
157.3: Myślę, że tak.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
157.1.: dla drugiego okresu T2=1,5s ; dla pierwszego okresu T1=3,5s
Wzór zatem wychodzi taki: epsilon=delta omega / delta t=(((2*3,14)/1,5)-((2*3,14)/3,5))/(1,5-3,5) i to daje około 1,2 rad/s^2, ale z minusem, więc trzeba dać wartość bezwzględną chyba. Sposób z wzorem na kąt jest jednak szybszy.
Dziękuję :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To zadanie jest trudne - poruszaliśmy je z tego powodu już w kilku tematach na naszym forum, więc pozwolę sobie podlinkować te tematy, bo tam jest już dosyć obszerna dyskusja, w której zapewne znajdziesz odpowiedzi na pp 1) i pp2):
https://forum.szkolamaturzystow.pl/wpis/1673901319-zz157
https://forum.szkolamaturzystow.pl/wpis/1674944875-zz1572
https://forum.szkolamaturzystow.pl/wpis/1711397071-zadanie-zz-1572
157.3: 1 - to po pierwsze, a po drugie to w początkowej fazie nie mamy w ogóle jeszcze jednej ustalonej wartości Umax, więc nawet nie bardzo wiadomo co tam by należało wrzucić.
Nie, tu nie mamy żadnego rezonansu. W istocie podobnie wyglądają drgania tłumione, ale tam amplituda drgań maleje w czasie, a nie rośnie tak jak tutaj.